CS Basics
计算机图形学基础
视角(view)和投影(projection)变换
Reference
- https://krasjet.github.io/quaternion/quaternion.pdf
- 视角和投影变换](https://zhuanlan.zhihu.com/p/362713511))
相机变换
变换的目的是将三维图形投影到二维平面上,通过光栅化获得像素的离散表征,给定相机的位置$e$,look at方向$g$(相机朝向),up方向$t$,获得一个新坐标轴,原点在e,y轴方向和t相同,z轴方向和g相反,视角变换矩阵$M_{view}$拆分成旋转$R_{view}$和平移$T_{view}$两项
考虑三维空间中的旋转,v分解为平行和垂直分量
仅仅旋转$v_\perp$,增加一个轴,记作
将变换后的$v_\perp^\prime$分解到w和$v_\perp$方向,得到
它们的关系是
因此新的旋转结果记作
旋转轴是一个单位向量
为了进一步讨论三维空间中的旋转,我们引入四元数,在这种情况下空间中任何一个点表示为
对应的共轭四元数为$s - v$,定义
两个四元数相乘记作
写成矩阵形式
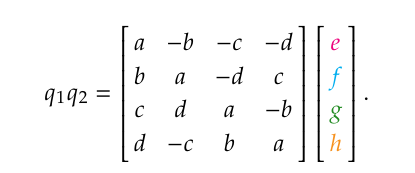
一对互逆的四元数满足
共轭四元数指的是
我们将$\ref{rotate_eq}$中的向量视为纯四元数
考虑垂直分量,写成纯四元数的形式
这是垂直向量的旋转公式,因此旋转被记作
对于单位向量u以及$q = [\cos\theta ,\sin\theta u]$,有$q^2 = qq = [\cos2\theta,\sin 2\theta u]$,并且q也是单位四元数,此时若$p =[\cos\frac \theta 2,\sin \frac \theta 2u]$,有$p^2 = q,p^{-1} = [\cos\frac{\theta}2 ,- \sin\frac\theta 2u]=p^*$
进一步写出
简化这个公式,介绍两个引理


$v^\prime$进一步优化为
这个公式表明对$v_\perp$做了正反两次旋转
最终写成终极形式,左乘四元数$a + bi +cj +dk$等价于乘以
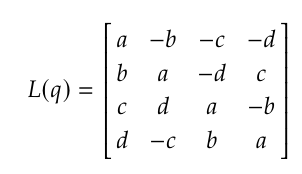
右乘等价于乘以矩阵
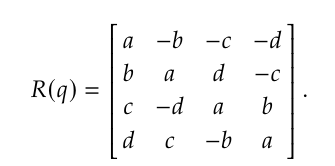
最终写成
最终旋转定理写成
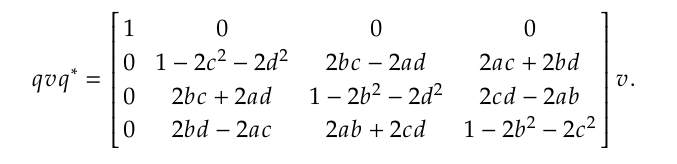
v最后一维是0,因此取上三角

alpha-blending
渲染过程中引入透明度的概念,考虑光线可以经过面元的情况,对于渲染管线,引入$\alpha$参数描述图层的透明度
深度缓冲(物体之间完全遮挡,不考虑物体的透明度)
为每个像素构建如下缓冲
- 深度缓冲,记录距离相机最近的面元深度
- 帧缓冲,记录像素点颜色
渲染对于每个面元先进行深度测试,舍去比Z-buffer更远的面元,深度写入更新Z-buffer
透明度混合:存在透明物体进行渲染
不透明不透明不透明不透明不透明*片元的深度值,渲染透明片元仍然应该进行深度测试,避免不透明物体在透明物体之前的情况
先渲染透明片元,在渲染不透明片元,因为透明片元不写到Z-buffer中,如何判断两者的深度,这里提供两条原则
- 透明片元按照深度逐个渲染
- 不透明片元优先于透明片元进行渲染(深度测试不为空)