Fourier_Analysis_Intro | Hexo

Fourier Analysis(Chapter 1 Intro)

Preliminary

Complex Sequence

定义复数序列$\{w_n\}$收敛于C当且仅当

$$\lim_{n\to \infty}|w_n-C|=0$$

复数序列极限是唯一的

复数Cauchy列定义为，对于复数序列$\{w_n\}$和$\forall \epsilon>0$，存在$N>0$，使得

$$|w_n-w_m|<\epsilon,\forall n,m>N$$

序列收敛当且仅当其为Cauchy列（实数部和虚数部都是Cauchy列）

级数的partial sum定义为

$$S_N = \sum_{n=1}^N z_n$$

给定一个实数列$\{a_n\}$，满足其和收敛，且对于$\forall n$均有

$$|z_n| \leq a_n$$

则$S_N$收敛

$\forall N,M,N>M$，有

$$|S_N - S_M| =|\sum_{n=M+1}^N z_n|\leq \sum_{n=M+1}^N |z_n| \leq \sum_{n=M+1}^N a_n\leq \epsilon$$

最后一步是因为$a_n$的偏序和满足Cauchy收敛准测

Complex exponential

Complex exponential定义为

$$e^z = \sum_{n=0}^\infty \frac{z^n}{n!},z\in C$$

1. 这个基数是收敛的，这是因为$|\frac{z^n}{n!}| =\frac{|z|^n}{n!}$,RHS显然收敛于0

2. \forall z\in \Omega,|z|\leq M$，这样$|\frac{z^n}{n!}|\leq \frac{M^n}{n!}$，因此有（维尔斯特拉斯判别法）

   $$|\sum_{n=0}^\infty \frac{z^n}{n!} - S_N |=|\sum_{n=N+1}^\infty \frac{z^n}{n!}|\leq {\sum_{n=N+1}^\infty \frac{M^n}{n!}}<\epsilon$$

   一致收敛性对应着函数列收敛，例如

   $$\sum_{n=0}^\infty \frac{1}{x+n} + x^2 \to x^2$$

   这是因为$\forall x,\lim_{n\to \infty}f_n(x)\to f(x)$，这被称为逐点收敛，一致收敛表明在每一点收敛速度相同，数,学上看，对于一个区间$[f(x) -\epsilon,f(x)+\epsilon]$在n足够大的时候都能保证$f_n(x)$落在这个区间中，即

   $$\forall n\geq N,x\in S,|f_n(x) - f(x)|<\epsilon$$

   一致收敛避免了形如$x^n \to 0,x\in (0,1)$的情况，因为$x\to 1$收敛速度变慢，但是如果仅考虑一个较小的区间$x^n$是一致收敛到0的

3. 在这种定义下，满足$e^{z_1+z_2} = e^{z_1} e^{z_2}$

   $$e^{z_1 }e^{z_2} =\sum_{n=0}^\infty \frac{z_1^n}{n!}\sum_{n=0}^\infty \frac{z_2^n}{n!} = \sum_{n=0}^\infty \sum_{m=0}^\infty \frac{z_1^n z_2^m}{m! n!} =\sum_{k=0}^\infty \frac{(z_1+z_2)^k}{k!}$$

4. 给定$z = iy$，则有$e^{z} = \sum_{n=0}^\infty \frac{i^n y^n}{n!} = (1 - \frac{y^2}{2!}+\frac{y^4}{4}+\cdots) + i(y - \frac{y^3}{3!}+\frac{y^5}{5!}) = \cos y + i sin y$

Problems

弹簧振子

简单简谐运动满足

$$-k y(t) =m\frac{d^2 y(t)}{dt^2}$$

得到

$$y(t) = a\cos ct+ b \sin ct,c = \sqrt{\frac km}$$

给定两个初始条件（位置和速度）可以求出a/b

$$y(0),y^\prime(0)$$

考虑空间上的行进波，在t时刻位置x处的振幅表示为

$$y = u(x,t)$$

standing waves**

t=0时初始profile表示为

$$y =\phi(x)$$

t时刻具有放大系数$\psi(t)$，$u$表示为

$$u(x,t) = \phi(x)\psi(t)$$

同比例缩小同比例缩小

traveling waves**，给定t=0时u的初始状态$F(x)$，在任意t时刻u相当于F在时间上的平移

$$u(x,t) = F(x-ct)$$

对于长度为L的string，将其分为N份$N\to \infty$，第n份坐标为$x_n =\frac{nL}N $，整个string被视为N个独立的质点组成的系统，每个指点仅能在垂直方向振动，定义$y_n(t)$为质点$x_n$在t时刻的垂直位置，即

$$y_n(t) = u(x_n,t),x_{n+1} - x_n= h=\frac L N$$

定义string的线密度为$\rho$，即每个质点的质量为$\rho h$，则

$$\rho h y^{\prime\prime}(t)$$

为质点$x_n$在t时刻收到的力，这个力来自相邻质点$x_{n-1}/x_{n+1}$，每个质点对相邻质点的力等于

$${(y_{n+1}-y_n)}\frac\tau h$$

类似于弹簧，考虑两个相邻质点对$x_n$的力，运动方程写成

$$\rho h y^{\prime\prime}_n (t) = \frac{\tau}{h}(y_{n+1}(t) + y_{n-1}(t) - 2 y_n(t))$$

RHS写成

$$u(x_n+h,t) + u(x_n-h,t)-2u(x_n,t)$$

对于$F(x)$，我们有

$$\lim_{h\to 0}\frac{F(x+h) + F(x-h) - 2F(x)}{h^2} = F^{\prime\prime }(x)$$

这个结论证明用到洛必达法则

$$\begin{aligned} LHS&=\lim_{h\to 0}\frac{F^\prime(x+h) - F^\prime(x-h)}{2h} \\ &=\lim_{h\to 0}\frac{F^{\prime\prime}(x+h) + F^{\prime\prime}(x-h)}{2} \end{aligned}$$

Q.E.D

因此运动方程写成

$$\rho h \frac{\partial ^2 u(x_n,t)}{\partial t^2}|_{t=t} =\tau h \frac{\partial^2 u(x,t)}{\partial x^2}|_{x=x_n}$$

得到

$$\frac{1}{c^2} \frac{\partial^2 u}{\partial t^2} = \frac{\partial^2 u}{\partial x^2}$$

为了简化考虑，不考虑系数(归一化)，得到

$$\frac{\partial^2 U}{\partial T^2} = \frac{\partial^2 U}{\partial X^2}\label{pde}$$

求解wave equation

对于Travelling wave（波沿着string匀速传播），假定$L=\pi$，此时满足

$$u(x,t) = F(x-t)$$

显然两个驻波之和仍然是驻波，给定两个二阶可微函数F/G，u(x,t)写成

$$u(x,t) = F(x+t) + G(x-t)$$

定义$\xi = x+t,\eta = x -t$，规定

$$v(\xi,\eta) = u(x,t)=F(\xi) + G(\eta)$$

则此时

$$x = \frac{\xi + \eta}{2},t = \frac{\xi -\eta}{2}$$

根据$\ref{pde}$，有

$$\begin{aligned} \frac{\partial u}{\partial t} & = \frac{\partial v}{\partial \xi}\frac{\partial \xi}{\partial t} +\frac{\partial v}{\partial \eta}\frac{\partial \eta}{\partial t}\\ &=\frac{\partial v}{\partial \xi} -\frac{\partial v}{\partial \eta}\\ \frac{\partial u}{\partial x} &= \frac{\partial v}{\partial \xi}+\frac{\partial v}{\partial \eta}\\ \frac{\partial ^2 u}{\partial t^2} &= \frac{\partial ^2 v}{\partial \xi^2} + \frac{\partial^2 v}{\partial \eta^2} -2 \frac{\partial^2 v}{\partial \xi \partial \eta}\\ \frac{\partial ^2 u}{\partial t^2} &= \frac{\partial ^2 v}{\partial \xi^2} + \frac{\partial^2 v}{\partial \eta^2} +2 \frac{\partial^2 v}{\partial \xi \partial \eta} \end{aligned}$$

得到

$$\frac{\partial^2 v}{\partial \xi\partial \eta} = 0$$

定义初始时刻string的状态满足

$$u(x,0) = f(x)$$

对于string的两端，满足

$$u(x,0) = u(x,\pi) = 0$$

初始每一点的速度为$g(x) =\frac{\partial u(x,t)}{\partial t}|_{t=0}$，因此得到

$$F(x) + G(x) = f(x)\Rightarrow F^\prime (x) + G^\prime(x) = f^\prime(x)\\ F^\prime(x)- G^\prime(x) = g(x)$$

解出$F^\prime(x),G^\prime(x)$，得到

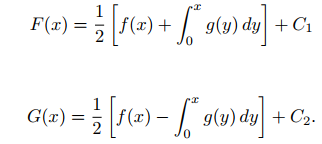
代入$u(x,t)$，得到

对于standwaves，有

$$u(x,t) = \phi(x)\psi(t)$$

根据波的通用性质$\ref{pde}$，得到

$$\phi^{\prime\prime}(x)\psi(t) = \phi(x) \psi^{\prime\prime}(t)\Rightarrow \frac{\psi^{\prime\prime}(t)}{\psi(t)} = \frac{\phi^{\prime\prime}(x)}{\phi(x)}$$

假定等于$\lambda$，得到

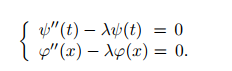
这对应的是三角函数

$$\psi(t) = A \cos mt + B \sin mt\\ \phi(x) = \hat A \cos mx + \hat B \sin mx$$

给定边界条件$\phi(0) = \phi(\pi) = 0$，得到$\hat A = 0$，并且m为整数，定义

$$u_m(x,t) = (A_m \cos m t+ B_m \sin m t)\sin m t$$

波具有可加性， 假设u/v是波动方程的解，那么$\alpha u + \beta v$也是波动方程的解（但是合成波不一定是驻波）

考虑$u_m(x,t)$的线性组合，记作

$$u(x,t) = \sum_{m=1}^{\infty} (A_m \cos mt+ B_m \sin mt) \sin m x$$

假定$u(x,0) = f(x)$，此时有

$$\sum_{m=1}^\infty A_m \sin mx = f(x)\label{Fourier_sin}$$

自然而然地，我们有如下问题，假设一个函数$f(x)$满足$f(0) = f(\pi) = 0$，能否求出一系列系数，完成上述分解$\ref{Fourier_sin}$，一个简单的方法是乘以一个正交kernel，利用

$$\int_0^\pi \sin mx \sin nx d x=\left\{ \begin{aligned} 0,m\neq n\\ \frac \pi 2, m= n \end{aligned} \right.$$

得到

$$A_n = \frac 2 \pi \int_0^\pi f(x)\sin nx dx$$

任意定义在$[-\pi,\pi]$上的函数表示为

$$F(x) = \sum_{m=1}^\infty A_m \sin mx + \sum_{m=1}^\infty A_m^\prime \cos mx =\sum_{m=-\infty}^\infty a_m e^{imx}$$

这里用到

$$e^{imx} =\cos {mx} + i \sin {mx}\\ \sin mx = \frac{e^{imx} - e^{-imx}}{2i},\cos mx = \frac{e^{imx} + e^{-imx}}{2}$$

因此有

$$a_m = \frac{A_m^\prime -i A_m}{2},a_{-m} = \frac{A_m^\prime + i A_m}{2}$$

Heat Equation

给定一块平面铁板，t时刻平面上$(x,y)$处温度记作$u(x,y,t)$，满足如下偏微分方程

$$\frac{\partial u}{\partial t} = \frac{\partial ^2u}{\partial x^2} + \frac{\partial ^2 u}{\partial y^2}$$

温度稳定，意味着

$$\frac{\partial u}{\partial t} = 0$$

对于圆盘，采用极坐标$u(r,\theta) = u(x,y),x = r\cos \theta,y = r\sin \theta$，满足

$$RHS=\frac{\partial ^2 u}{\partial r^2} + \frac 1 r \frac{\partial u}{\partial r} + \frac{1}{r^2}\frac{\partial ^2 u}{\partial \theta^2} = 0\\ r^2 \frac{\partial ^2 u}{\partial r^2} + r\frac{\partial u}{\partial r} = -\frac{\partial ^2 u}{\partial \theta^2}$$

假设$u(r,\theta) = F(r) G(\theta)$，有

$$\frac{r^2 F^{\prime\prime}(r) + rF^\prime(r)}{F(r)} = -\frac{G^{\prime\prime}(\theta)}{G(\theta)} = \lambda$$

得到

$$\lambda = m^2 \\ G(\theta) = A e^{im\theta} + B e^{-im\theta}$$

1. $m = 0$解由两个base线性组合$F(r) = 1/\log r$
2. $m\neq 0$解由两个base线性组合$F(r) = r^m /r^{-m}$

显然$\log r/r^{-m},m >0$都是不reasonable的$r\to 0$，因此解记作

$$u_m(r,\theta) = r^{|m|} e^{im\theta}$$

合成解记作

$$u(r,\theta) = \sum_{m=-\infty}^{\infty}a_m r^{|m|}e^{im\theta}$$

考虑边界温度$f(\theta)$，有

$$u(1,\theta) = \sum_{-\infty}^{\infty}a_m e^{im\theta} = f(\theta)$$

级数乘法

讨论

$$(\sum_{i=1}a_i)(\sum_{i=1}b_i)$$

写成

$$\sum_{n=1} c_n,c_n = \sum_{i+j= n+1}a_i b_j$$

$\sum c_n$为两个级数的Cauchy乘积

两个级数收敛，Cauchy乘积可能发散

$$a_n = b_n = (-1)^n\frac{1}{\sqrt n}$$

两个级数收敛，且Cauchy级数收敛则Cauchy级数收敛于两者之和极限乘积

$$\sum_i ^n a_i \to A,\sum_i ^n b_i \to B\Rightarrow \sum_i c_n = AB$$

引理1 $a_n \to a\Rightarrow\frac{\sum_i^n a_i}{n}\to a$

对于$a = 0$证明即可

引理2 $a_n \to a,b_n \to b\Rightarrow \frac{c_n}{n}\to ab $

证明b=0且$a_n$有界即可

定理证明

考虑三个partial sum

$$A_n = \sum_{k=1}^n a_k,B_n = \sum_{k=1}^n b_k ,C_n = \sum_{k=1}^n c_k$$

显然 $C_n$是$a_n$和$B_n$的Cauchy乘积

$$C_n = a_1 B_n + a_2 B_{n-1} +\cdots + a_n B_1$$

显然

$$\frac 1 N \sum_{n=1}^N C_n = \frac 1 N (A_n B_1 + A_{N-1}B_2+\cdots +A_1 B_N)$$

利用引理2得到$\sum_{n=1}^n $收敛于AB