Information Theory:Mathematical Basic and Introduction | Hexo

Information Theory(Introduction and Math Basics)

Introduction

1. Define:信息可以消除Uncertainty of Receiver
2. Representation of Information for store and convey
   1. language and 0-1 code
3. Codebook/Dictionary代表信息编码的规则（编码和解码的依据）

Compactness of Code

如何用尽量少的代价编码相同的信息(Best Design of Codebook,compactness)

按照概率编码代价最低按照概率编码代价最低按照概率编码代价最低按照概率编码代价最低按照概率编码代价最低代价最低**

能否在不知道最优设计的前提下计算最低编码代价（measure of information）

Three Assumptions of information

1. Monotonicity in event probability，一个随机事件发生的概率越大，那么这件事真正发生所包含的信息价值越小；相反一个概率上不太可能的事件真正发生才能引起人们的注意(surprise)
2. Additivity：两个独立事件信息量直接相加
3. Continuity：信息是概率的连续函数

唯一满足这种定义的数学形式是概率倒数取log $\log_2\frac 1 p$

给定4个event(A,B,C,D)，发生概率分别为$\frac 1 2,\frac 1 4,\frac 1 8,\frac 1 8$，对应的entropy为$1,2,3,3$，平均编码长度为

$$\frac 1 2 * 1 + \frac 1 4 * 2 +\frac 1 8 * 3 + \frac 1 8 * 3 = \frac 7 4$$

给定编码方案

$$A = 0\\ B=10\\ C=110\\ D=111 \label{optim。，}$$

是否存在歧义？

Other Assumption

编码成本和编码长度的2次方成正比

$$L(t) =\sum_{z\in Event} Pr(z) 2^{t\times l(z)}\Leftrightarrow \min\log_2 \sum_{z}Pr(z)2^{t\times l(z)}$$

t是常数

Renyi Entropy

Data Transmission over noisy channel

传送一段信息，有一定概率receiver收到的信息发生错误，物理层传送一个bit时间固定。

为了避免传送一个bit数据出现错误，需要在物理层重复传递数据若干次(Channel Code Bit)，例如

$$1\to 111\\ 0\to 000$$

接收端物理层接收三个物理bit，根据大数法则(2个1则判断逻辑层传送1)判断逻辑上传送的bit，用三次Channel Code Bit代替One Information bit

传送一个Information Bit需要三个传输Channel Code Bit时间($\frac 1 3 $ code rate)

Shannon在论文中用Transmission efficiency(Channel Code rate)指代这种现象(1/3 zero-one information symbol per channel usage)

Information Transmission System

给定事件z，Shannon在论文中将Transmission过程抽象为若干函数

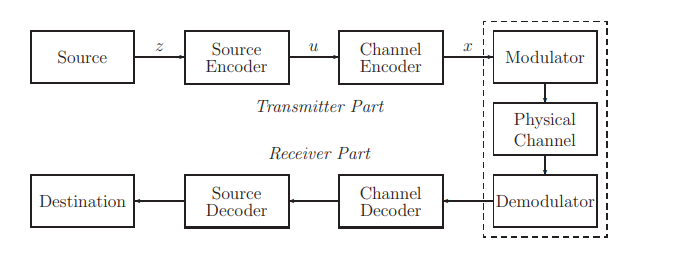
1. bit}$
2. Channel Encoder编码u为Channel Codewords $x = g(u)$,redundancy code

map event to Channel Codeword $x = g(f(z)) = h(z)$,joint source channel coding

Source Encode

设计最好的Source Encoder和Channel Encoder

最好的压缩方法Source Entropy为1，每个bit而言出现0，1概率均为$\frac 1 2$，每个Bit携带的Entropy为1

反之输出的$\{U\}\in \{0,1\}$并不能保证每个bit都是Uniformly distributed，它德Entropy

$$H(U) = p\log_2 \frac 1 p+(1-p)\log_2 \frac{1}{1-p}$$

$P(U=0) = p$

代表现在编码方式每个bit携带的信息量

Channel Encode

定义错误率，假定Source Encoder输出包含k个bit，假设序列$u_1u_2\cdots u_K$被送入Channel Encoder中，根据对Optimal Source Encoder的讨论，输入包含$2^K$种可能性，每种可能性出现的概率是uniform的，定义error

$$error =\frac{1}{2^K}\sum_{u_1u_2\cdots u_K}Pr(error|u_1u_2\cdots u_K)$$

Arbitrary Small Error Probability

在固定Code Rate的情况下，要求Information Transmission Error足够小(Arbitrary Small Error Probability)

这种设计不考虑编码的复杂性，实际上Error越小编码长度越高

Channel Capacity

有杂讯的管道存在一个Channel Capacity，这个值的含义是传输信息的速度大于这个值出错的概率可以Arbitrary Small，大于这个值错误率必然为1

Maximum Reliable Transmission Code Rate，这仅仅和杂讯分布相关

Mutual(Sender and Receiver) Information

1. 好的Channel Code能够increase certainty of channel output to channel inputs
2. Shannon借助Entropy衡量Uncertainty，Input Uncertainty和Output Uncertainty之差被定义为Mutual Information（Consensus of Sender and Receiver）

A Toy Example

输入信息U经过编码生成X，杂讯相当于一个自然先验，假定Noisy Channel的输入

$$X\in \{(a,a),(a,b),(b,a),(b,b) \}$$

Noisy Channel output满足，对于输入$X = (V_1,V_2)$，保持$V_1$不变，$V_2\to b$

1. Input Uncertainty，计算输入的Entropy(离散4分布随机变量)
2. Output Uncertainty，第二维度始终为b，因此Uncertainty仅仅来自$V_1$

Shared Uncertainty $V_1$

给定四个事件$E_i,i=1,2,3,4$，最好的Source Encoder一定为

$$E_1:aa\\ E_2:ab\\ E_3:ba\\ E_4:bb$$

篡改篡改篡改篡改篡改篡改篡改篡改篡改篡改**为b，导致$E_1/E_2，E_3/E_4$无法区分，将其映射为

$$E_1:(a,d),(a,d)\\ E_2:(a,d),(b,d)\\ E_3 : (b,d),(a,d)\\ E_4 : (b,d),(b,d)$$

Overview of Suprema and Limits

1. 实数集合有上界则存在最小上界
2. 上界有则唯一
3. extend real number(包含$\infty$和$-\infty$)

Properties of Suprema

1. Suprema扩展(extend real system)

$$\sup A =\left\{ \begin{aligned} &-\infty ,A=\phi\\ &\infty,A\ not\ bounded \end{aligned} \right.\Rightarrow \forall a\in A,a\leq \leq A$$

1. Suprema定义(Arbitrary Small)

$$-\infty <\sup A< \infty\to \forall \epsilon >0,\exists a_0 \in A,s.t \ a_0 \geq \sup A -\epsilon$$

实数集合中的值可以和上确界任意逼近

Suprema and Maximum

$\sup A\in A\to \max A = \sup A$

Supremum of a set and Channel Coding Theorem

为了证明$\alpha$是Set A的Supremum

1. Forward/Direct Part $\alpha -\epsilon$对于A是可达的$\Rightarrow \forall \epsilon>0,\exists a_0\in A,a_0> a-\epsilon$
2. Converse Part $\alpha$可以bound住A中所有元素 $\forall a\in A\to a\leq \alpha$

如果$\alpha$是Maximum，只需要证明

1. $\alpha$在A中可达
2. $\alpha$ bound了A所有元素

Boundedness and Suprema Operation

1. Bounded :是否存在上界和下界
2. Bounded集合需要满足 $\exist k,\forall a\in A,|a|\leq k$
3. Monotone Property 子集/全集Sup/Inf的关系

Set Operations

Addition of A and B

$$A+B = \{c\in \R:c = a+b,\forall a\in A,\forall b\in B\}$$

Scaler of A

$$k\cdot A = \{\forall c\in R,c = k\cdot a\forall a\in A\}$$

Product of A and B

$$A \cdot B = \{c,c=ab\forall a\in A,b\in B\}\\ \sup(a\cdot B)\leq \sup A \cdot \sup B$$

Supremum/Infimum for monotone functions

non-decreasing function f

$$\sup\{x\in R,f(x) < \epsilon\} = \inf\{x\in \R:f(x)\geq \epsilon\}\\ \sup(x\in \R,f(x)\leq \epsilon) = \inf(x\in \R:f(x)>\epsilon)$$

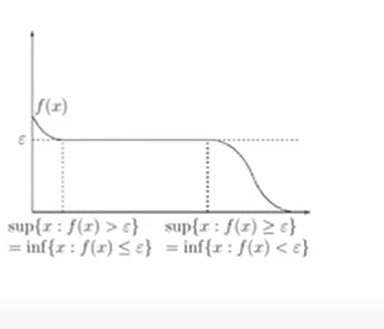
但是不能保证

$$\sup\{x\in \R:f(x)\leq \epsilon\} = \sup\{x\in \R:f(x)<\epsilon\}$$

Probability and Random Process

Probability Space

$\sigma-Field$定义$\mathcal F$为一个非空集合$\Omega$子集组成的集合，定义$\mathcal F$为$\alpha-Field$如果满足如下三条性质（$\sigma-Field$是对集合的操作）

1. $\Omega\in F$
2. F对于补集操作是封闭的 $A\in \mathcal F\to A^c \in \mathcal F,A^c = \{w\in \Omega,w\notin A\}$（事件和反事件）
3. F对可数个集合的并集操作是封闭的，对于若干给定可数集合$A_i\in \mathcal F,\bigcup_{i=1}^\infty A_i\in F$（事件$A_i$中至少发生一个）

简单地说$\sigma-Field$定义了全集上可以计算概率的子集集合

给定一个集合$\Omega$，最小的$\sigma-Field$为$(\Omega,\phi)$，最大的$\sigma-Field$为$\Omega$所有子集组成的集合

Probability space定义关注于一个tuple $(\Omega,\mathcal F,P)$，P是一个set到实数的映射

Probability Space Probability被定义为$(\Omega,\mathcal F,P)$组成的tuple($\Omega$：全集，$\mathcal F:\alpha-Field$，P子集映射为[0,1]实数的量度)$\to$概率公设

1. $P(A) \in [0,1]$

2. $P(\Omega) = 1$

3. 不相交的可数集合$A_i$概率满足

   $$P(\bigcup_{k=1}^\infty A_k) = \sum_{k=1}^\infty P(A_k )$$

如何在连续样本空间找到满足Kolmogorov公设的概率函数$P$（Borel集合在概率论上的意义)

给定$\R$的子集能否计算概率，答案是否定的，例如下面的例子

等价关系用于建立对象之间的关系，需要满足1.$x=x$ 2. $x=y\Rightarrow y=x$ 3. $x=y,y=z\Rightarrow x =z$，由此延伸出等价类的概念

不同等价类之间只可能有两种关系

1. 相等
2. 完全不相交

将[0,1]区间划分为等价类并集

$$[0,1] = \cup_{\alpha}\epsilon_\alpha$$

等价类定义为

$$\forall x,y\in [0,1],x-y\in k,k\in Q,x = y$$

两者相差为有理数，显然这是等价关系（只要两个数差为有理数）

等价类定义为

$$[x] = \{y|y-x\in Q\}$$

显然可以将实数区间划分为无数个不相交的等价类（两个无理数的差可能是无理数，也可能是有理数）

$$R = \bigcup_{\alpha}[\alpha]$$

有理数单独构成一个等价类，无理数划分为多个等价类

每个等价类中选择落在[0,1]的一个元素构成Vitali集合，这个集合是不可测的

定义[-1,1]上的有理数集合为(这一定是可数的)

$$q_1,q_2,\cdots,$$

定义Vitali集合的偏移

$$V_k = V+ q_k$$

因为$\forall v\in V,v\in [0,1]$，因此

$$\forall v_k \in V_k,v_k\in [-1,2]$$

必然有

$$[0,1]\subset \bigcup_k V_k \subset [-1,2]$$

因此$\bigcup_k V_k$的测度应该落在[1,3]区间内

无穷个不相交测度相等集合并集测度要么为0，要么为$\infty$，不成立

可以定义概率的集合可以定义概率的集合可以定义概率的集合可以定义概率的集合集合**，这个集合中每个事件都是可以用概率刻画的，满足

1. 全集/空集在事件集合中
2. 某个事件在是概率可测的，那么这个事件的补集也是概率可测的
3. 可数事件是概率可测的，这些事件同时发生(交集)，至少有一个发生(并集)也是可测的

对于离散事件定义概率上可测的事件是比较容易的，因为可以遍历其幂集合，对于连续空间，比如说定义在[0,1]上的随机变量，是否任意取[0,1]的一个子集都能找到其对应的概率呢？答案是否定的

上述讨论的整体脉络是

1. 给定全事件集合A
2. 给定A的Sigma-Field，表明哪些A的子集是可测的
3. 对于可测A子集，定义概率映射F将其映射到实数（测度）

在利用分布函数在$\R$上定义概率，分布函数$F:\R\to [0,1]$满足

1. $\forall a\leq b \Rightarrow F(a)\leq F(b)$
2. $\lim_{x\to x_o^+} F(x) = F(x_0)$（为什么只约束了右连续）
3. $F(-\infty) = 0,F(\infty)=1$

Borel $\sigma-Field$

定义实数子集组成的集合，其中每个子集都是概率可度量的

包含所有开闭区间

Random Variable

随机变量被视为事件全集$\Omega$子集到实数[0,1]的映射 $X:\Omega\to \R$

Random Process

1. 若干Random Variable

2. 所有Random Variable定义在同一个random space上

   1. 基于同一套Event Space
   $$P(X_1\leq t_1,X_2\leq t_2) = P(\{w|X_1(w)\leq t_1\} \bigcap \{w|X_2(w)\leq t_2\} )$$
   1. 可度量集合基于$\sigma-Field$定义，因此它们的交集也是可测的

$$\{x_t,t\in I\}$$

T-Invariant（时间角度刻画离散随机过程的性质）

给定事件E和操作T，如果E是T-invariant，则应该满足

$$TE \subseteq E\\ TE = \{Tx,x\in E \},Tx = T(x_1,x_2,\cdots,) = (x_2,x_3,\cdots)$$

时序平移时序平移*，Time Invariant的事件具有时间不变性（无论从什么时候开始观测都得到同样的结果）

给定事件

$$E = \{1111\cdots,0111\cdots,0011\cdots\}$$

关心的事件：多次随机试验所有硬币均为正面，第一次为反面其余均为正面，前两次为反面其余均为正面

一定有$TE\subseteq E$，这样E被称为T-invariant

1. 通过T操作集合E越来越小了（收敛于1111…）
2. 如何延拓不T-invariant的集合使之称为T-invariant集合
3. in-decomposable，经过无限次T操作得到的最小集合中的所有元素，我们希望关注不随着时间变化的事件集合，事件全集被划分成若干等价集合

等价状态等价状态等价状态等价状态*，即我们不能删除group中的任何一个元素，否则将会破坏其T-invariant的特性

Ergodic

定义切割的反函数

$$T^{-1}E = \{x\in X^\infty:Tx\in E \}$$

$X^\infty$指的是长度为无限的事件序列，例如010101…

例如

$$E = \{0101\cdots,1111\cdots\}\\ T^{-1}E = \{1010\cdots,1111\cdots \}$$

注意到，如果$E = \{0101\cdots,1010\cdots\}$，则有$T^{-1} E = E$，这种情况我们称为E是Ergodic set

时序不变性时序不变性变性**，满足

$$T^{-1} E = E$$

的集合，这种情况下

$$TE = T(T^{-1}E ) = E,T^\lambda E = E$$

对于two-sided random process(Reindex)

$$\cdots X_{-2}X_{-1}X_0X_1X_2\cdots\to TE = X_{-2} \to X_{-1}$$

对于one-side random process

$$X= \{X_1,X_2,\cdots\}$$

1. Memoryless(无记忆性) 随即过程每个随机变量都是iid的，无需记住历史上时序信息
2. stationary(稳态) 任意选择一个事件集合，在任意时刻选择随机变量X，落在集合上的概率完全相同
3. ergodicity(遍历性) 随机过程的时间均值等于空间均值（关心的Event在时间上具有周期性）
   1. 对随机过程 $x_1,x_2,\cdots$，统计第j个变量的均值，需要进行多次实验得到$x_j^1,x_j^2,\cdots$计算其平均
   2. 同样一次实验计算计算一个轨迹上的均值$mean(x_1,x_2,\cdots,x_n)$，两者相等

Ergodicity实际上是来自热力学的概念，为了统计某个容器内物体的平均运动速率，有两种做法

1. 对于单个分子，在不同时间点测量其速率，计算平均值
2. 某个时间点采样容器内若干分子计算其平均值

两种算法得到的期望是相同的

不可切分不可切分不可切分的事件集合，一般是时间平移的收敛结果

给定两个集合，集合A

$$101010\cdots\\ 010101\cdots$$

显然满足时间不变性，并且有

$$\lim_{n\to \infty} \frac{\sum_i^n x_i}{n } = \frac 1 2$$

集合B

$$10010010\cdots\\ 0010010\cdots\\ 010010\cdots$$

满足时间不变性，并且

$$\lim_{n\to \infty}\frac{\sum_i^n x_i}{n} =\frac 1 3$$

$A\bigcap B=\phi$，这是一个封闭体系

同样，对于无线序列组成的随机过程

$$X= (x_1,x_2,\cdots)$$

定义事件

$$A =\{(x_1,x_2,\cdots)| \lim_{n\to \infty}\frac{\sum_i x_i}{n}= 0.1\}\\ B =\{(x_1,x_2,\cdots)| \lim_{n\to \infty}\frac{\sum_i x_i}{n}= 0.1\}$$

两个Set必然不相交

考虑连续随机过程$X(t)$，遍历性意味着任意取时间点$t_1$，并且取时间点$t_2,\cdots,t_n$，必然满足

$$\frac{\sum_i E[X(t_i)]}{n}收敛$$

这并不意味着$E[X_{t_1}] = E[X_{t_2}]=\cdots =E[X_{t_n}]$

随机过程的教科书上所说的平稳过程指的是随机过程随机变量的某些特性不随时间变化

1. 期望E[X(t)]为常数，协方差Cov[X(s),X(t)]是t-s的函数（宽平稳）
2. 任意有限维随机过程中向量的的分布均相同分布均相同**，则随机过程为严平稳过程

$$pdf(X_{t_1+\tau},\cdots,X_{t_n+\tau})= pdf(X_{t_1},\cdots,X_{t_n})$$

Y是一个随机变量，随机过程$X_t$满足

$$X_{t} = \cos(t+Y)$$

1. 如果$Y=U [0,2k\pi]$，那么$X_t$显然是Stationary的
2. 对于其它非均匀分布，$X_t$不是Stationary的

遍历性涉及另一个概念：随机过程的时间平均，对于离散随机过程和一次观测，定义n个观测时间的平均

$$\overline X_n = \frac {\sum_{i=1}^n x_i}{n}$$

均方收敛于均方收敛于均方收敛于$\tau$，即

$$\lim_{n\to \infty}E(\overline X_n - \tau)^n = 0$$

同理提出ensemble average的概念，个人觉得是多条轨迹取平均，一个Wiki上的例子，给定两枚硬币

1. 正反两面概率相等
2. 只有正面

随机选择一枚硬币，投掷硬币，显然ensemble average为

$$\frac 1 2 \times \frac 1 2+ \frac 1 2\times 1 = \frac 3 4$$

对于单个实验，测量的time average为$\frac 1 2$或1，但是这个随机过程显然是stationary的

Point-wise ergodic theorem

给定静态随机过程$X_n$，给定实数函数$f(\cdot)$，满足

$$E[f(X_n)] < \infty$$

随机变量Y**，使得

$$\lim_{n\to \infty} \sum_{k=1}^n f(X_k)$$

和Y分布相同（均值可能不是常数而是随机变量）

对于Ergodic过程，一定有

$$\lim_{n\to \infty} \frac 1 n \sum_{k=1}^n f(X_k) = E[f(X_1)]$$

Ergodic过程时间均值一定会收敛于某个常数

Stationary ergodic random source

测量测量测量测量每个随机变量的概率分布

Markov Chain

贝叶斯公式揭示了联合概率分布和条件概率分布的关系

$$P_{X,Y,Z}(x,y,z) = P_X(x) \cdot P_{Y|X}(y|x) \cdot P_{Z|X,Y}(z|y,x)$$

马尔科夫性简化了条件概率之间的变量依赖

$$P_{X,Y,Z}(x,y,z) = P_X(x) \cdot P_{Y|X}(y|x) \cdot P_{Z|Y}(z|y)$$

一个重要的结论是

当Y已知时，X和Z相对于Y条件独立，即

$$P(x,z|y) = P(x|y)P(z|y)$$

因此$X\to Y\to Z$和$Z\to Y\to X$本质上没什么不同

Irreducible

对于任意状态$x^k,y^k\in X^k$，存在重复周期j，使得

$$Pr(x_j^{k+j-1}=x^k|x_j^k = y_^k)>0$$

Time-invariant

状态转移的概率不随时间改变

$$Pr(x_2=x|x_1=x^\prime) = Pr(x_3=x|x_2=x^\prime)$$

Aperiodic

对于同一状态x，定义状态周期

$$d(x)= gcd(n|Pr(x_{n+1}=x|X_1=x)>0)$$

特殊情况

$$\forall n,Pr(x_{n+1}=x|x_n= x)=0,d(x)=\infty$$

1. d(x)=1$
2. Markov Chain是aperiodic等价于所有状态都是aperiodic的

Stationary

自回归性自回归性自回归性自回归性自回归性**

$$\pi(y) = \sum_x \pi(x)Pr(x_{n+1}=x|x_n=1)$$

Irreducible的Markov Chain一定存在唯一的$\pi$