Deep Bisimulation for Control | Hexo

表示学习：如何区分输入信号中不重要的部分

背景介绍

基于重建误差的特征表征

传统的表示学习通过Encoder-Decoder架构，损失函数为重建误差，提取中间层表征作为数据特征，这样必然导致环境过拟合，本文提出了一种表征方法克服这一缺点

何为相似状态？

两个不同MDP的状态是相似的当且仅当

1. 状态执行同一个action的奖励是相似的(Reward距离)
2. 下一个状态的距离(Dynamic距离)

$$d(s_i,s_j) = \max_{a\in \mathcal A}(1 - c)|R_{s_1}^a -R_{s_j}^a | +c W_1 (P_{s_i}^a ,P_{s_j}^a;d)\label{bmatric}$$

状态转移实际上是概率，这里用的是Wassertein距离

特征空间上的距离$\parallel z_1-z_2\parallel_2$正比于原始输入空间中的Reward距离+Dynamic距离间上的距离$\parallel z_1-z_2\parallel_2$正比于原始输入空间中的Reward距离+Dynamic距离**

相关工作：Representation Learning in Reinforcement Learning

Reconstruction Based Representation

基于重建误差的缺点之前已经描述，一切工作同时训练Encoder和环境模型，这些方法很难准确预测长期的环境变化

Contrastive Based Representation

对比学习中的特征提取器仍然需要获得图像的全部信息

Bisimulation

状态在动作空间的等价性状态在动作空间的等价性状态在动作空间的等价性*

$$R(s_i,a)= R(s_j,a),\forall a\in A\\ P(G|s_i,a) = P(G|s_j,a)\forall a\in A,\forall G\in S_B$$

行为相关性行为相关性行为相关性行为相关性行为相关性行为相关性行为相关性行为相关性行为相关性行为相关性关性**，这个函数的定义参见$\ref{bmatric}$

Method(DBC,Deep Bisimulation for Control)

表示学习部分

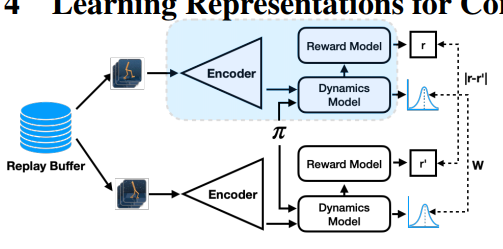
Encoder记作$\phi$，之前损失函数$\ref{bmatric}$中取max的操作导致其很难应用于高维空间，本文提出直接在Encoder的输出空间上构造损失函数

$$J(\phi) = (\parallel z_i - z_j\parallel_1 - |r_i-r_j| -\gamma W_2(P(\cdot|\overline{z_i},a_i)\parallel P(\cdot|\overline{z_j},a_j)))$$

计算reward distance和dynamic distance实际上都是stop gradient的，$P$是一个probabilistic dynamic model，根据latent embedding输出高斯分布

本文的第二个贡献是将两阶段训练融合在一起，Dynamic的训练需要根据next timestep的状态得到$z_{t+1}$，它实际上在Latent Space上对下一个状态的分布做预测

强化学习训练

Q函数和策略都是基于Encoder产生的Latent Encoder所生成

数学上证明泛化能力

Pseudometric

定义Pseudo Metric空间(X,d)，X是一个set，d是一个函数

$$d:X\times X\to R_{\geq 0}$$

d是pseudometric，当且仅当满足三条性质

1. $d(x,x) =0$
2. $d(x,y)= d(y,x)$
3. $d(x,z)\leq d(x,y) + d(y,z)$

例子

给定空间$\mathcal F(X)$为所有实数函数组成的空间$f:X\to \R$，对于X中给定的一点$x_0\in X$，定义两个函数之间的距离

$$d(f,g) = |f(x_0) - g(x_0)|$$

Wasserstein Distance

reference Wasserstein Distance

这是一种刻画概率分布的方式，先回顾一些现有的概率度量(概率度量应该满足对称性，因此KL散度被排除)

$$Hellinger:\sqrt{\int (\sqrt p - \sqrt q)^2}\\ L_2:\int (p-q)^2$$

不能刻画分布几何特征的相似性

定义

W-距离定义了两个分布之间转化的代价，对于两组离散分布P,Q

$$P = P_1,P_2,\cdots,P_n\\ Q = Q_1,Q_2,\cdots,Q_n$$

约定第0 step开销$\delta_i = 0$，第i step的开销为

$$\delta_i = \delta_i + P_i- Q_i$$

总代价为

$$W = \sum|\delta_i|$$

对于连续情况，我们定义Coupling of two distributions $(\mu,v)$，它是一个二维分布，分布的边缘分布等于$\mu,v$

$$\gamma\in \Tau(\mu,v)\\ \int \gamma(x,y) dy = \mu,\int \gamma(x,y) dx = v$$

连续分布的Wasserstein距离定义为分布族上的优化问题，需要找到分布上期望的下确界

$$W_p(u,v) = (\inf_{\gamma \in \Tau (\mu,v)} E_{(x,y)\in \gamma} d(x,y)^p)^{\frac 1 p}$$

Learn More

SmoothL1 Loss

连续的损失函数

$$Smooth_{L1}(x,y) =\left\{ \begin{aligned} & 0.5(x_i-y_i)^2,if\ |x_i-y_i|<1\\ & |x_i -y _i| - 0.5 \end{aligned} \right.$$

什么是一个好的工作

1. 有新意
2. 有效(有所提升)
3. 研究问题(尝试可能会失败)/工程问题(尝试一般是有效的)