Domain Generalization(Review,Methodology and Theory) | Hexo

Domain Generalization(Theory and Methodology)

Theory Analysis of DA and DG

Reference

1. Blog of Theory of DA
2. Intro of Domain Adaptation Theory

DA

对于一个二分类问题，给定Source Domain和Target Domain上的映射函数（最优映射）

$$h^{*^s},P_X^s,h^{*^t},P_X^t:\mathcal X \to [0,1]\\$$

定义两个分类器$h,h^\prime$在Source Domain上的difference

$$\epsilon^s(h,h^\prime) = E_{x|P_X^s}[|h(x) - h^\prime(x)|]$$

定义risk of classifier h in source/target domain

$$\epsilon^s(h) = \epsilon^s(h,h^{s^*}),\epsilon^t(h) = \epsilon^t(h,h^{t^*})$$

希望用$\epsilon^s(h)$将$\epsilon^t(h)$ bound住，第一个定理表明了sample-distance，difference和risk of classifier之间的关系

需要度量两个特征空间分布上的距离，先介绍$\mathcal A$距离，定义为

$$d_{\mathcal A}(P_X^s,P_X^t) =\sup_{A\in X}|P_X^s(A) - P_X^t(A)|$$

给定输入空间的子集，计算两个概率分布落在子集上的概率，取相差最大值，假设我们的样本分布是两个高斯分布，定义映射函数为

$$h(z) = 1,z\leq 0\\ h(z) = 0,z\geq 0$$

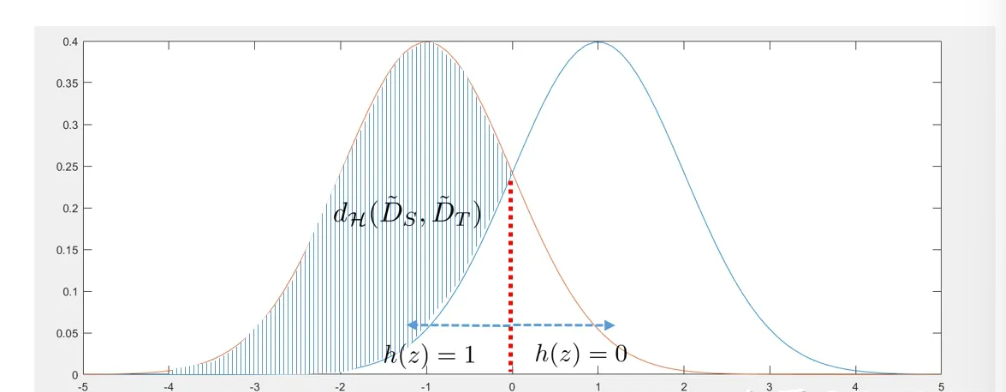
$\mathcal A$距离对应两个积分中相差的部分

现在缩小输入空间X的范围，选择输入空间中所有label为True的样本空间，记作

$$A = I(h) =\{z\in Z|h(z) = 1,h\in \mathcal H \}$$

只在这个输入空间的子集上搜索，退化为$\mathcal H$距离

随后定义$\mathcal H\Delta \mathcal H$距离，给定Source/Target Domain，定义$\mathcal H$为Binary Mapping组成的集合，利用Risk of classifier定义距离，给定两个Classifier，要求在source/target Domain上判断值相差最大

$$d_{H\Delta H} = 2\sup_{h_1,h_2\in H} |Pr_{x|P_X^s}(h_1(x)\neq h_2(x)) - Pr_{x|P_X^t}(h_1(x)\neq h_2(x))|$$

还是上面的例子，如果定义

$$h_1(x)=\left\{ \begin{aligned} &x\leq -1\\ &x\geq -1 \end{aligned} \right.\\ h_2(x)=\left\{ \begin{aligned} &x\leq 0\\ &x\geq 0 \end{aligned} \right.\\$$

则$Pr_{x|P_X^s}(h_1(x) \neq h_2(x))$为$\mathcal N(-1,1)$积分中[-1,0]的区间，后者为$\mathcal N(1,1)$积分[-1,0]的区间

注意这里的距离定义与ground truth无关

误差上界定理：Target Domain上的泛化误差$\epsilon_T(h)$一定被Source Domain上的泛化误差$\epsilon_S(h)$和Domain距离Bound住

$$\epsilon_T(h)\leq \epsilon _S(h) +d_{\mathcal H\Delta \mathcal H}(P_X^s,P_X^t) +\lambda\\ \lambda =\epsilon_S(h^*) + \epsilon_T(h^*)\\ h^* =\arg\min_{h\in \mathcal H} \epsilon_S(h) + \epsilon_T(h)$$

$h^*$是在Source/Target Domain上错误率最低的映射

误差上界定理表明了Target Domain risk被三项Bound住

1. Source Risk
2. Source-Target Distribution Divergence
3. Complexity of $\mathcal H$（和分类器本身有关）

Domain adaptation理论主要解决了如下问题

1. Error in Source Domain和Error in Target Domain之间满足何种关系？能否通过优化前者保证后者也被bound住
2. 如何刻画不同Domain之间的距离，Domain距离对模型在Source/Target Domain上的性能差异有无影响

将基于Source Domain和Target Domain数据分布得到的最优分类器记作$f_S,f_T$，两个Domain记作$D_s,D_T$，那么Source Domain Error $\epsilon_S(h)$和Target Domain Error $\epsilon_T(h)$之间满足Bound

$$\epsilon_T(h) \leq \epsilon_S(h) + d(D_S,D_T)+\min\{E_{D_S}|f_S(x) - f_T(x)|,E_{D_T}|f_S(x) - f_T(x)| \}$$

Proof

$$\begin{aligned} \epsilon_T(h) &= \epsilon_T(h) +\epsilon_S(h) - \epsilon_S(h) + \epsilon_S(h,f_T) - \epsilon_S(h,f_T)\\ &\leq \epsilon_S(h) +|\epsilon_S(g,f_T) - \epsilon_S(h)| + |\epsilon_T(h) - \epsilon_S(h,f_T)| \end{aligned}$$

第二行最右两项表明两个判别器在同一Domain上并不Agree，写成

$$\begin{aligned} |\epsilon_S(h,f_T) - \epsilon_S(h)| &=|E_{D_S}[|h-f_T| - |h-f_s||]|\\ &\leq E_{D_S} ||h-f_T| - |h-f_S|| \end{aligned}$$

可以证明$RHS\leq d_1(D_S,D_T)$

Review of Risk Upper Bound

1. 选择合适的有代表性的样本，降低Domain Divergence
2. 学习Domain Invariant Representation

Problem Setting of DG

1. Distribution not same
2. Test Domain Can not be accessed

Methodology

基于数据变换实现Domain Generalization

对于transform后的数据$x\to x^\prime$，假定其具有label不变性

$$\min_{x,y|D} E_{x,y}[l(h(x),y)] + E_{x^\prime,y}[l(h(x^\prime),y)]$$

Data Augmentation Based Method

1. 基于Domain Randomization模拟环境的多样性，一个研究方向是如何去除对泛化没有帮助的randomize
2. 对抗数据增强保证了数据增强得到的结果具有高可用性

Data Generation-based DG

1. Mixup Strategy（线性插值作为数据增强的方式，插值系数来自$\Beta$分布）
2. MMD Distance for Domain discrepancy measurement
3. Wasserstein Auto-Encoder

基于表示学习

学习领域无关表示

1. 学习Representation Kernel
   1. Transfer/Domain-Invariant Component Analysis
2. Domain Adverse Training
   1. DANN同时学习Domain-Invariant和Label-Relevant的表征
3. Explicit feature alignment，设计损失函数（对比学习）显式刻画不同Domain的Feature距离

Invariant Risk Minimization

对于不同Domain获得的表示

$$E_1,E_2,\cdots,E_M$$

基于此构建M个Classifier用于标签推断

$$C_1,C_2,\cdots,C_M$$

因果关系因果关系因果关系因果关系因果关系因果关系因果关系因果关系因果关系因果关系系**

基于解耦表征

解耦表征的一般形式：借助Domain-Generalized Representation学习Representation到Label的映射，构建Domain Specific/General Mapping $g_s,g_c$

$$\min_{g_c,g_s,f} E_{x,y}[l(f(g_c(x),y))] + \lambda l_{reg} +\mu l_{recon}([g_c(x),g_s(x)],x)$$

关键在于如何设计$l_{reg}$以控制表征的解耦

基于集成学习

针对每个Domain学习一个模型

$$f_1(x),f_2(x),\cdots,f_N(x)$$

利用多个模型做加权

$$f =\sum_i^N w_i f_i(x)$$

两个损失函数分别代表判别距离$\mathcal L_c$和Domain分类距离$L_{domain}$

Video Introduction

基于数据的领域泛化

Context Aware Randomization

Context相当于条件变量，基于某种先验分布进行数据增强

Adversarial Data Augmentation

1. Cross Grad（需要进一步阅读）
2. ADV Augmentation，给定若干Source Domain $D_1,D_2,\cdots,D_K$，希望学到的模型具有最大程度的泛化能力(Worst Case)，定义

$$\min_{\theta}\sup_{P}[E_P[l(\theta;(X,Y)):D_\theta(P,P_0)\leq \rho]]$$

给定Domain分布的邻域，找到一个分布使得risk最大

基于表征的领域泛化

Feature Alignment

借助现有Distance用于评估Representation是否是Domain Invariance

Invariant Risk Minimization（进一步阅读）

之前的工作先要求不同Domain在表征学习得到的分布尽量相似，随后基于表征学习一个分类器。IRM的思路正好相反，它要求先学习一个好的分类器，再要求特征空间不同Domain的Representation尽量一致

解耦表征

Undo Bias

权重分为Shared和Specific

$$w_i = w_0 + \Delta w_i$$

DIVA

Representation解耦为和Domain(d)有关的Feature以及和Label(y)有关的Feature(借助不同Decoder实现)

基于不同学习策略

Meta Learning

多个Source Domain组成的数据集通过随机采样生成Meta-Train/Meta-Test Domain，从Meta-Train迁移到Meta-Test上

Ensemble Learning

学习不同权重的线性组合