optimize transport
最优传输问题
推土机距离
Problem Setting
给定n个土堆,包含$s_i$量的土,给定m个坑,每个坑可以容纳$d_j$量的土。土和土堆表示为
假设
定义距离矩阵$M\in \R^{n\times m}.m_{ij}$表示将单位质量的土从堆i搬到坑j需要的代价,希望得到一个传输矩阵$P\in \R^{n\times m}$,使得代价
最小,显然矩阵P应该满足
这是一个线性规划问题
推广推土机距离到概率分布
假设s,r都是概率分布,即
最优推土机距离可以表示为两个离散概率分布(维度不一定相同)之间的距离。这种方法被广泛用在无监督学习或者半监督学习的loss函数设计上,比如对比学习中,希望同一个instance通过不同transform得到的概率分布更加相似
熵正则的最优传输问题
定义:熵正则
矩阵P的熵定义为
矩阵熵越大,说明对应的分布越分散,不希望分布过于集中,因此损失函数记作
不加正则项,线性规划问题最优解一定落在多边形定点上,导致分布不均衡,在这种情况下可以用Sinkhorn迭代得到最优解
Sinkhorn算法
不断在两个向量$u\in \R^n,v\in \R^m$上迭代,初始设置为均匀分布
迭代
$e^{\lambda M}$是一个$n\times m$的矩阵,除法代表两个向量逐个元素相除
,v^,v^^*$,这种情况下最优传输矩阵写成
对比学习中最优传输
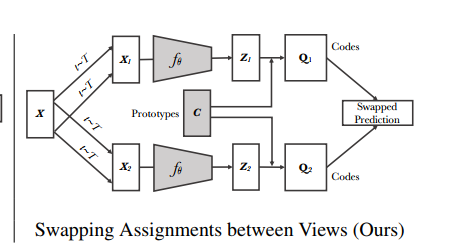
一个Batch包含B个样本,经过feature extraction和两种数据增强后生成一对正的embedding(嵌入维度是m)
通过在线聚类(计算一个cluster内K-means)得到K个聚类中心
一组$z_s,z_t$在聚类中心c下计算的对比损失记作
$q_s,p_t\in \R^K$来自$z_s,z_t$,可以认为原始embedding在K个中心作用下的投影,$p_t^i$计算为
向量$q_s$的求解转化为最优传输问题,实际上将$z_s^i$生成的q向量记作$q_{i} =(q_{i}^1,q_{i}^2,\cdots,q_{i}^k) \in \R^K$记矩阵
Q是如下最优传输问题的解
$C\in \R^{m\times K},Z\in \R^{m\times B},C^TZ = \R^{K\times B},Q^TC^T Z = \R^{B\times B}$
实际上求解的是代价矩阵为$C^T Z,K\to B$的最优传输问题,对应的原分布为K,B上的均匀分布