heterogenous offline rl | Hexo

Paper Collection(Multiple Policies Optimization in Offline RL)

多策略集构成的数据集可能让基于策略约束的offline rl算法出现退化，总结一下基于mixture policies做offline rl的方法

reference

1. offline rl from heteroskedastic data 提出了一个toy model
2. Real World Offline Reinforcement Learning with Realistic Data Source
3. V2AE,policy structure

Importance of Policy Structure of Offline RL

本文通过控制latent variable，得到了一个state-action space下的diverse policies，本文提出的基于diverse policy学习的算法可以减少offline rl中的critic loss

定义Mixture policy

一个policy有latent variable z控制

$$\pi(a|s) = \sum_z \pi(z|s)\pi(a|s,z)$$

选择latent variable的gating policy根据Q值最大的latent variable得到

$$z = \arg\max_z Q_w(s,\mu_\theta(s,z))$$

目标函数被定义为policy evaluation函数在动作-状态空间上的期望

$$J(\pi) = E_{s\in D,a\in \pi}[f^\pi(s,a)]\\ f^\pi(s,a) = \exp(Q^\pi(s,a)) ,A^\pi(s,a),\exp{(A^\pi(s,a))}\tag{objective function}\label{objfunc}$$

Maximizing Variational Lower Bound to train an actor

希望获得$\ref{objfunc}$的lower bound，写出它在latent variable z下的变分下界，假设

1. policy evaulation function参数w，记作$\hat {f^\pi_w}(s,a) $
2. deterministic policy function参数$\theta$，记作$\pi_\theta(a|s)$
3. behavior policy记作$\beta(a|s)$

推导$J(\pi)$的对数下界为

$$\log J(\pi) = E_{(s,a)\in D}[\log \pi_\theta(a|s)\hat {f_w^\pi}(s,a)] - E_{(s,a)\in D}[\log \beta (a|s) \hat {f_w^\pi}(s,a)]\tag{variation lowered bound of expectation return} \label{loss return}$$

参数策略$\pi_\theta(a|s)$的变分下界写成

$$\begin{aligned} \log \pi_\theta(a|s) &\geq -D_{KL}(q|\phi(z|s,a)\parallel p(z|s)) +E_{z|p(z|s,a)}[\log \pi_\theta(a|s,z)]\\ &=l_{cvae}(s,a;\theta,\phi) \end{aligned}\tag{variational lower bound of conditional log-likelihood}\label{loss policy}$$

RHS本质上是一个cvae的loss函数，policy conditional variable是latent variable，先验分布并非一个无参数的分布，而是Q值的softmax

$$p(z|s) = \frac{\exp {Q_w(s,\mu_\theta(s,z))}}{\sum_z \exp{Q_w(s,\mu_\theta(s,z))}}$$

Q值根据double-clip计算得到，$\ref{loss policy}$第一项是离散分布的KL散度，第二项是predictive loss，这样得到$\ref{loss return}$的lower bound表示

$$L_{ML}(\theta,\phi) = \sum_{i=-1}^N f^\pi(s_i,a_i)l_{cvae}(s_i,a_i;\theta,\phi)\tag{CVAE loss}\label{CVAE}$$

用于训练CVAE，优化这个损失函数可以优化cvae，

Train the critic for a mixture of deterministic policies

带有gating policies的Bellman Equation写成

$$\Tau Q_z = r(s,a) + \gamma E_{s^\prime}Q_{z}(s^\prime,\mu(s^\prime,z^\prime))$$

Algorithm

1. 为什么通过优化$\ref{CVAE}$可以学习到好的actor？

因为CVAE计算KL散度中需要计算encoder产生的离散分布，离散分布和Q值和actor计算的动作有关

1. 为什么是max CVAE的损失函数

本质上$\ref{CVAE}$并非CVAE真正的损失函数，第一项

$$-KL(\pi_\phi(z|s_i,a_i)\parallel p(z|s_i))$$

描述的是分布距离，KL散度的意义告诉我们希望尽量减少KL散度，也就是max它的相反数，第二项

$$E_{z|p(z|s_i,a_i)}[\log \pi_{\theta}(a_i|s_i,z_i)]$$

完全可以用重构距离描述

如何在离散分布采样中反向传播(无需，直接求解期望即可)

对于状态$s_i$，计算它在k组latent variable下的动作，记作

$$a_1^i,a_2^i,\cdots,a_k^i$$

计算loss采取加权

$$loss(s_i,a_i) = \sum_{j=1}^k (a_j^i - a_i)^2 p_j$$

Code Implementation

构造CVAE

$$CVAE(E_\phi,D_\psi),E_\phi:(s,a)\to p\in \R^{|Z|}\\ D_\psi:s\times z\to a$$

Actor-Critic

$$Critic:Q_w:s\times a\to 1\\ Actor:A_\theta(s,z):s\times z\to a$$

采样实现反向传播，从先验分布$p(z)$中采样z，计算$A_\theta(s,z)$，希望最小化重构距离，loss表示为

$$loss (s,a) = \sum_z p(z) (D_\psi(s,z) - a)^2$$

Experiment

toy环境(稀疏奖励)

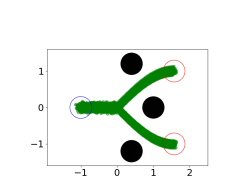
D4RL Benchmark

Behavior Estimation from Multi-Source Data for Offline Reinforcement Learning

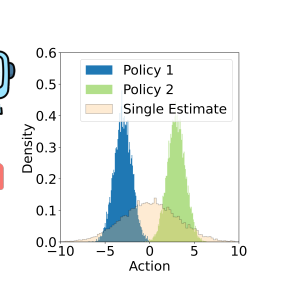
Multi-Source Trajectory带来的问题是在同一个状态倾向于采取不同的动作，本文通过从异质数据集中建模多个策略解决数据异构型的问题。本文提出的基于latent variable的model-learning算法将policy和trajectory嵌入到低维空间中，并尝试从低维空间表示中重建action

Task:Behavior Estimation

给定数据集$D=\{\tau_m\}$，输出生成数据集的behavior policy

$$\max_{\theta_b} E_{(s,a)\in D}[\log b(a|s;\theta_b)]$$

medium-replay data来自多个策略

Problem Statement(Behavior Estimation from Multi-source Data)

对于包含M条trajectory的数据集$D= \{\tau_m\}_{m=1}^M$，可以认为它采样自不同策略，希望输出一个K个策略组成的behavior set $\mathcal B=\{b_k \}_{k=1}^K$。同时生成轨迹到策略的映射矩阵

$$G\in \{0,1\}^{M\times K},$$

$G_{u,v} = 1\Rightarrow$轨迹$\tau_u$由策略$b_v$生成

From persepective of Possibility Graph

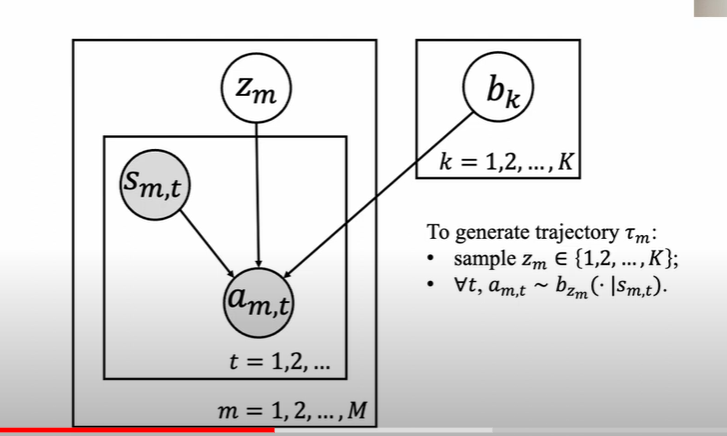
Latent-Variable Model

假设数据集来自K个策略，生成策略的过程可以分成两个部分

1. 选择对应的latent variable $z_m$
2. 基于策略$b_{z_m}$采样生成轨迹

这里一条基本假设是每条轨迹均来自单一策略

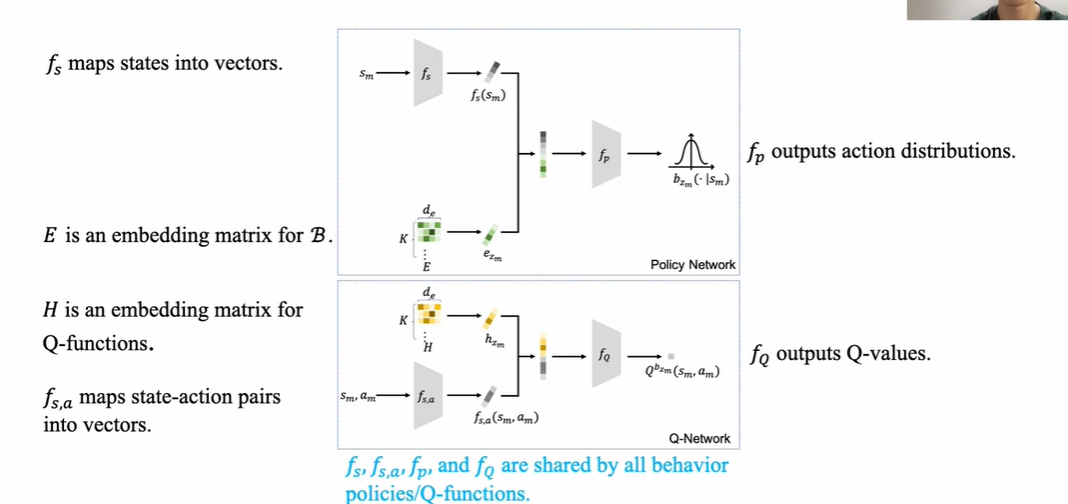
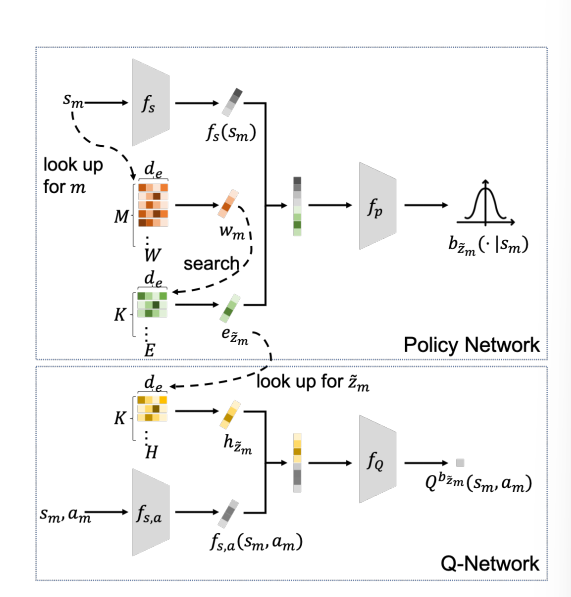
Policy Network和Q-Network包括三个矩阵

1. $W\in \R^{M\times d_e}$，将$\mathcal D$中的每个trajectory映射到一个长度$d_e$的嵌入
2. $E\in \R^{K\times d_e}$是每个policy的嵌入
3. $H\in \R^{K\times d_e}$是每个策略的Q function的嵌入矩阵
4. 构建policy network：$f_s$将state嵌入到low-representation，和E矩阵中对应的张量concat送入policy encoder $f_p$中输出policy的分布
5. 构建Q network：将state-action pair嵌入到low-representation $f_{s,a}$，和policy embedding做concat送入$f_Q$

真实异质数据集

Parameter Updated

$z_m$作为当前state $s_m$选择的策略下标，它的先验分布根据$e_j,w_m$内积计算得到

$$q(z_m=k|s_m,a_m)=\left\{ \begin{aligned} &1\quad k = \arg\max_j e_j^T w_m\\ &0\quad else \end{aligned} \right.\tag{priority distribution of $z_m$}\label{prior}$$

通过action reconstruction学习trajectory embedding matrix $W\in \R^{M\times d_e}$，希望通过$f_s,w_m,e_{z_m}$重建$a_m$，因此损失函数为

$$L_{rec} = l(f_p(f_s(s_m),e_{z_m}),a_m)+l(f_p(f_s(s_m),w_m),a_m)$$

$e_{z_m},w_n$都是$d_e$维向量，可以作为actor输入，W矩阵用于获取policy矩阵中policy嵌入

同时根据$\ref{prior}$，选择的$e_j$应该在内积上和$w_m$尽量相似，因此第二个损失函数写成

$$L_{com} = 1 - w_m^T e_{z_m}$$

第三项损失函数是TD error，对于输入的transition $(s_m,a_m,r_m)$，通过policy net计算出一个动作分布，记作

$$b_{z_m}$$

从这个分布中采样计算TD error

$$L_Q = E_{a^\prime|b_{z_m}}[(r_m + \gamma Q^{b_{z_m}}(s_m^\prime,a^\prime) - Q^{b_{z_m}}(s_m,a_m))^2]$$

总的loss记作

$$L = L_{rec} +\alpha L_{com} + L_Q$$

BRAC-v

BRAC-v是最简单的一类policy penality算法，基于learned policy和behavior policy之间的差异进行约束，它的Actor-Critic Loss记作

$$L_{critic} = E_{a^\prime|\pi(\cdot|s_m^\prime)}[r_m +\gamma (Q^\pi(s_m^\prime,a^\prime) -\beta D(\pi,b,s_m^\prime)) - Q^\pi(s_m,a_m)]^2\\ L_{actor} = E_{a|\pi(\cdot|s_m)}[\beta D(\pi,b,s_m) - Q^\pi(s_m,a)]$$

这个损失函数实际上在DDPG基础上加上策略距离

策略距离$D(\pi,b,s)$定义为

$$D(\pi,b,s) = E_{a|\pi(\cdot|s)} [\log \pi(a|s) - \log b (a|s)]\tag{policy distance}\label{pdistance}$$

1. $\pi$ learned policy
2. b behavior policy

multi-source data条件下用$\ref{pdistance}$很难刻画策略距离，针对multi-source data的假设，我们在从一个轨迹$\tau_m$中学习时，希望使用对应轨迹的概率分布刻画它和Learned Policy之间的距离

参考本文中学习$f_s,f_p,s_{s,a}$的思路，希望学习两个representation

$$e_\pi,h_\pi\in \R^{d_e}$$

前者是learned policy representation，后者是对应的Q function representation

Experiment

数据集

基于3个D4RL环境，每个环境收集四个数据集

1. random(random policy)
2. medium(medium RL agent)
3. medium-replay(训练Agent过程中收集的数据)
4. medium-expert(medium+expert收集经验)

Heterogeneous-k dataset

基于SAC保存若干checkpoints收集的数据集