Overview Of Stein Fourier Analysis(Chapter 2)

一个定义在[0,L]上的函数的Fourier Coefficients写成

$$a_n = \hat f(n)= \frac 1 L \int_0^L f(x) e^{-\frac{2\pi i n x}{L} }dx$$

对应的Fourier Series of f写成

$$\sum_{n=-\infty}^{\infty} a_n e^{\frac{2\pi i nx}{L}}$$

定义Fourier Series of f的partial sum

$$S_N(f)(x) =\sum_{n=-N}^N \hat f(n) e^{2\pi i nx /L}$$

本章提出的第一个问题是，需要为f添加什么约束，使得

$$\lim_{N\to \infty} S_N(f) = f$$

怎么定义函数级数收敛于一个函数？

给出几个偏序和的粒子

三角多项式

$$D_N(x) = \sum_{n=-N}^N e^{inx} = \frac{w^{-N} - w^{N+1}}{1 - w} = \frac{\sin ((N+\frac{1}{2})x)}{\sin \frac x 2},w = e^{ix}$$

Poisson kernel

$$P_r(\theta) = \sum_{n=-\infty}^\infty r^{|n|} e^{in\theta} = \frac{1 - |w|^2}{|1-w|^2},w = re^{i\theta}$$

这种情况下函数级数收敛指的是

$$\lim_{N\to \infty} \int_{-\pi}^\pi |S_N(f)(\theta) - f(\theta)|^2 d\theta \to 0$$

讨论收敛性之前，本文讨论了傅里叶级数的唯一性，首先证明了一下结论

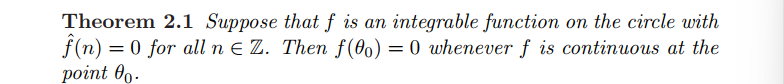
为0的条件为连续/可积且所有傅里叶系数均为0，根据以上结论得到以下推论

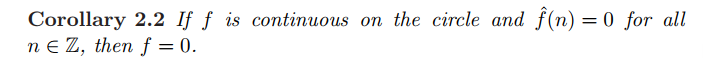
这个结论相比2.1缺少了可积的假设，同理我们得到偏序和的收敛性质

$\sum_n |\hat f(n)|<\infty$保证了Fourier级数绝对一致收敛，因此存在极限$g(\theta)=\lim_{N\to \infty}\sum_{n=-N}^N \hat f(n)e^{in\theta}$，g和f的傅里叶级数相同，因此得到$f-g$恒等于0

进一步，下列定理说明了可微函数傅里叶系数的bound，有如下结论

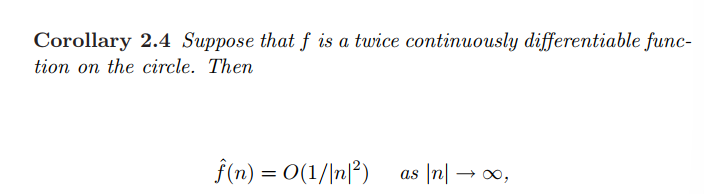
利用有界性+分部积分得到，同理还有

$$\hat f^\prime(n) = in \hat f(n)$$

下面介绍两个重要的概念：卷积和good kernel

卷积

两个周期为$2\pi$的可积函数f/g卷积被定义为

$$f*g (x) = \frac 1{2\pi} \int_{-\pi}^\pi f(y)g(x-y) dy = g*f(x)$$

Fourier Series $S_N(f)(x)$可以写成三角多项式和f的卷积

$$S_N(f)(x) =\sum_{n=-N}^N \hat f(n) e^{inx} = (f*D_N)(x)$$

这是因为

$$\begin{aligned} S_N(f)(x) &=\sum_{n=-N}^N \frac 1 {2\pi}\int_{-\pi}^\pi f(y) e^{-iny} dy e^{inx}\\ &= \frac 1 {2\pi}\int_{-\pi}^\pi f(y) \sum_{n=-N}^N e^{in(x-y)} dy\\ &=f * D_N(x)\ \end{aligned}$$

卷积有两个很好的性质

1. $f*g$是连续的（仅仅要求f/g可积）
2. $\hat{f*g}(n) = \hat f(n) \hat g(n)$

Good kernels

Fourier级数写成f和三角多项式的卷积，我们希望有如下性质

$$\lim_{N\to \infty} f * D_N = f\label{conv_estimation}$$

这种情况下可以用三角函数的线性组合拟合原始周期函数，为了获取上述的kernel，我们定义满足如下三个条件的kernel序列$\{K_n(x)\}$为good kernel

1. 正则$\forall n\geq 1,\frac 1{2\pi}\int_{-\pi}^\pi K_n(x) dx =1$

2. 有界$\int_{-\pi}^\pi|K_n(x)|dx \leq M$

3. 对于$\forall \delta>0$，满足随着N增大，$K_n(x)$落在$\delta \leq |x|\leq \pi$区间上的概率越来越小

   $$\int_{\delta \leq |x|\leq \pi}|K_n(x)| dx \to 0,n\to \infty$$

满足这三个条件，我们有

$$\lim_{n\to \infty} f*K_n(x) = f(x)$$

这里的收敛指的是逐点收敛，对于

$$\lim_{n\to \infty} f_n(x) = f(x)\Leftrightarrow \forall x,\lim_{n\to \infty}|f_n(x) - f(x)| = 0$$

但是不幸的是$D_N(x)$并不满足这个性质（不满足条件2），因此如果希望得到逼近$\ref{conv_estimation}$，需要重新定义函数项级数的收敛

$$\begin{aligned} D_N(\theta)& = \frac{w^{-N} - w^{N+1}}{1 - w},w = e^{i\theta}\\ \int_{-\pi}^\pi |D_N(\theta)| d\theta & = \int_{-\pi}^\pi| \frac{\sin ((N+\frac{1}{2})\theta)}{\sin \frac \theta 2}|d\theta\\ &\geq \int_{-\pi}^\pi \frac{2}{|\theta|}|\sin ((N+\frac 1 2)\theta)| d\theta\\ &\geq \int_0^\pi \frac{|\sin (2N +1)\theta|}{\theta} d\theta \end{aligned}$$

最后进行积分换元$(2N+1)\theta\to \theta$，得到

$$RHS =\lambda\int_0^{(2N+1)\pi} \frac{|\sin s|}{s}ds=\sum_{k=0}^{2N}\int_{k\pi}^{(k+1)\pi} \frac{|\sin s|}{|s|}$$

得证$D_N(\theta)=O(\log N)$

修改函数项级数收敛的定义，引入Cesaro/Abel求和

Abel/Cesaro Sumability

重新定义级数收敛，例如对于$\{(-1)^n\}$这样的级数，显然按照$s_n= \sum_{k=0}^n (-1)^k$的概念$s_n$是不收敛于一个实数s的，重新定义其N th Caesaro mean

$$\sigma_N = \frac{s_0+s_1+\cdots +s_{N-1}}{N}$$

显然$\sigma_N \to \frac 1 2$，对于求和$s_n = S_N(f) = \sum_{n=-N}^N a_n e^{in x},a_n = \frac 1 {2\pi}\int_{-\pi}^\pi f(x) e^{-inx} dx$的情况，同样定义N th Cesaro mean of the Fourier Series

$$\begin{aligned} \sigma_N(f) (x)& = \frac{S_0(f) + \cdots +S_{N-1}(f)}{N} \\ &= \frac{f*D_0(x) + f*D_1(f) + \cdots +f*D_{N-1}(f)}{N}\\ &=\frac{f*(D_0+D_1+\cdots +D_{N-1})}{N} \end{aligned}$$

定义Fejer Kernel

$$F_N(x) = \frac{\sum_{i=0}^{N-1}D_i(x)}{N} =\frac 1 N \frac{\sin^2 \frac{Nx}{2}}{\sin^2 \frac x 2}$$

这是一个good kernel，因此有

$$\lim_{N\to \infty} \sigma_N(f)(x) = \lim_{N\to \infty} f*F_N(x) = f(x)$$

问题：上述收敛在每一点x都成立，是一致收敛吗？

every pointevery pointevery pointevery pointy point** of continuity of f

上述证明针对的是一个离散函数级数$f_1,f_2,\cdots,f_n$，Abel means将其推广到连续场景，对于$\forall r\in [0,1)$和级数$c_k$，定义其Abel sum

$$A(r) = \sum_{k=0}^\infty c_k r^k$$

如果

1. $A(r)$对于$\forall r\in [0,1)$收敛，并且(注意这是一个左闭右开的区间)
2. $\lim_{r\to 1}A(r) =s(相当于将n\to \infty推广到了r\to 1，实际上的good kernel的条件)$

则称$\sum_{k=0}^\infty c_k$是Abel Summable的，并且$A(r)$被称为级数的Abel means，但是这并不意味

$$\lim_{N\to \infty} \sum_{k=0}^N c_k = s$$

反例是$(-1)^k(k+1),k=0,1,2,\cdots,\infty$，同理这个序列也不是Cesaro summable的

$$s_n =\left\{\begin{aligned} &2n+1,n=2k\\ &-2n,n=2k+1 \end{aligned}\right.,k=0,1,2,\cdots$$

得到

$$\sum_{i=0}^n s_i =\left\{ \begin{aligned} & 0,n=2k+1\\ & \frac{n+1}2,n=2k \end{aligned} \right.$$

显然$\frac{\sum_{i=0}^{n-1}s_i}{n}$不收敛

为什么有了Cesaro sum还要引入Abel sum

Poisson kernel and Dirichlet proble in the unit disc

假设$c_n=a_n e^{in\theta}$，对应Fourier Series中的某一项，则对应的Abel sum写成

$$A_r(f)(\theta) = \sum_{n=-\infty}^{\infty} r^{|n|} a_n e^{in\theta} = (f*P_r)(\theta)\\ P_r(\theta) = \sum_{n=-\infty}^\infty r^{|n|} e^{in\theta} = \frac{1 - r^2}{1 -2r\cos\theta +r^2}$$

并且$P_r(\theta)$是good kernel，这意味着，对于$\forall \delta>0$，对于积分

$$\psi(r) =\int_{\delta \leq |\theta|\leq \pi}P_r(\theta) d\theta$$

都存在

$$P_r(\theta)\leq \frac{1 -r^2}{c_\delta}$$

此时

$$\lim_{r\to 1}\psi(r) = 0$$

这个kernel满足

$$\lim_{r\to 1} f*P_r(\theta) = f(\theta)$$

Poisson kernel和f的卷积逐点收敛

回到热传导问题，温度分布$u(x,y)$应该满足

$$\Delta u = 0\\ u|_{x^2 + y^2} = f(boundary)$$

将$(x,y)\to (r,\theta)$，我们有

$$u(r,\theta) = \sum_{n=-\infty}^\infty a_n r^{|n|} e^{in\theta} = A_r(f)(\theta) = (f*P_r)(\theta)$$

其中$a_n = \frac{1}{2\pi} \int_{0}^{2\pi} f(\theta) e^{-in\theta}d\theta$，这个解是Abel Summable的（good kernel满足第二条性质）

以上解满足三条性质

1. $\Delta u = 0$ 直接计算梯度即可
2. $f$在$\theta$处连续，则有$\lim_{r\to 1}u(r,\theta) =f(\theta)$
3. 对于连续函数f，上述$u(r,\theta)$是满足单位圆盘上热传导方程的唯一解

$u(r,\theta)$其实可以用过分离变量法得到$f(r)g(\theta)$