Information Measures of Discrete Systems | Hexo

Information Theory(Information Measures of Discrete Systems)

随机事件E信息量$\Tau(E)$的衡量满足三个条件

1. 是随机事件E发生概率$Pr(E)$的单调递减函数
2. $T(E)$是$Pr(E)$的连续函数
3. 独立事件$E_1,E_2$交集的量度等于两者量度之和$T(E_1\bigcap E_2) = T(E_1)+T(E_2)$
4. $T(E)\geq 0$，了解一个事件不会让不确定度降低

唯一符合以上公设的数学形式写成

$$I(p)= -c \log_b (p)$$

$c,b>0$

启发启发启发启发启发，显然概率越小的事件发生价值越大

Entropy视为事件发生的信息量的期望

$$H(X) = E[T(X)]=\sum P_X(x) \log_b \frac{1}{P_X(x)}$$

介绍一些数学结论

$$1-\frac 1 x\leq \ln x \leq x-1\\ \log_D (x)\leq \log_D(e)(x-1)$$

Upper Bound of Entropy

$$H(X)\leq \log_2 |X|$$

Uniform的概率分布entropy最大

Log-sum inequality

$$\sum_i a_i \log_D \frac {a_i}{b_i} \geq \sum_i a_i( \log_D \frac{\sum_i a_i}{\sum_i b_i})$$

prove

$$\sum_i a_i (\log _D \frac{\sum_i a_i}{\sum_i b_i} -\log_D \frac{a_i}{b_i})\leq \sum_i a_i(\frac{b_i\sum a_i}{a_i \sum_i b_i}-1)=0$$

Joint Entropy刻画了多个随机变量的信息增益

$$H(X,Y) = E_{x,y|P_{X,Y}}[-\log_2 P_{X,Y}(X,Y)]$$

Conditional Entropy定义类似，给定发送端数据X条件下，接收端得到的信息增益

$$H(Y|X) = E_{x}[H(Y|x)]$$

Chain Rule

$$H(X,Y) = H(X) + H(Y|X)$$

共有信息量=发送端信息量+传输端条件信息量

考虑三者传输

graph LR
X-->Y
X-->Z
Z-->Y

满足

$$H(X,Y|Z) = H(X|Z) + H(Y|X,Z)\\ p(x,y|z) = \frac{p(x,y,z)}{p(z) }= \frac{p(x,y,z)\times p(x,z)}{p(x,z)\times p(z)}= p(y|x,z)p(x|z)$$

Side Information告诉我们引入一个新的conditional side information不会让系统不确定性增加

$$H(Y|X)\leq H(Y)$$

同理

$$H(X_1,X_2|Y_1,Y_2)\leq H(X_1|Y_1) + H(X_2|Y_2)$$

Mutual information用于表示H(Y|X)和H(X|Y)的交集

$$I(X;Y) = H(X) - H(X|Y) = H(X)+ H(Y) - H(X,Y)=D(P_{X,Y}\parallel P_X P_Y)$$

$I(X;Y )= 0$代表X和Y相互独立，这代表我们的信道不能正确传输信息（信道能传送的信息）

考虑多个输出端的情况

$$I(X;Y,Z)=D(P_{X,Y,Z}\parallel P_X P_{Y,Z})$$

X同时送给Y和Z，满足

$$I(X;Y,Z)= I(X;Y) + I(X;Z|Y)\\ I(X;Z|Y) = \sum_y P_Y(y) I(X|y;Z|y)=\sum_u P_Y(y) D(P_{(X,Y)|z}\parallel P_{X|y}\times P_{Z|y})$$

以上用到了条件互信息，可以写成

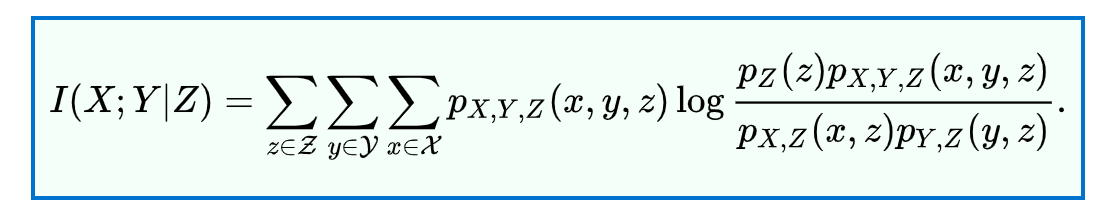
显然可以拆分成

$$\begin{aligned} I(X;Y|Z) &= \sum_{x,y,z} p_{X,Y,Z}(x,y,z)\log \frac{P_{X,Y,Z}(x,y,z)}{P_{Y,Z}(y,z)}\\ &+\sum_{x,y,z}P_{X,Y,Z}(x,y,z) \log \frac{P_Z(z)}{P_{X,Z}(x,z)} \\ &=D(P_{X,Y,Z}\parallel P_{Y,Z}) - D(P_{X,Z}\parallel P_Z)\\ &=I(X;Y,Z) - I(X,Z) \end{aligned}$$

扩展到多到一的场景

$$H(X_1,X_2,\cdots,X_n;Y) = \sum_{i=1}^n H(X_i;Y|X_1,\cdots,X_{i-1})$$

Entropy也遵循类似的Chain Rule

$$H(X_1,X_2,\cdots,X_n) = \sum_{i} H(X_i|X_1,X_2,\cdots,X_{i-1})\leq \sum_i H(X_i)$$

同理考虑多对多的传输

$$I(X_1,X_2;Y_1,Y_2)\leq I(X_1;Y_1) + I(X_2;Y_2)$$

取等号满足

$$P(y_2,y_1|x_2,x_1) = p(y_2|x_2)p(y_1|x_1)$$

时序上互相独立

一起传输不如一对一传输的效率高