subspaceofpolicies
Paper Reading——Learning A Subspace of Policies for Online Adaptation in Reinforcement Learning
Few shot Adaptation
小样本学习基于有少量有监督数据和大量无监督数据的场景
问题背景
学习环境和测试环境存在区别,本文讨论一种算法能够在多种环境上进行泛化。
- 提到参数空间下策略的一个子集
- 参数空间应该指的是环境的参数,应该是将环境作为一种变量送给RL算法学习到environment adaptation policy
- 一种方式将环境特征/信息作为meta data送给学习器训练,但是对于只有一种环境的情况容易产生过拟合
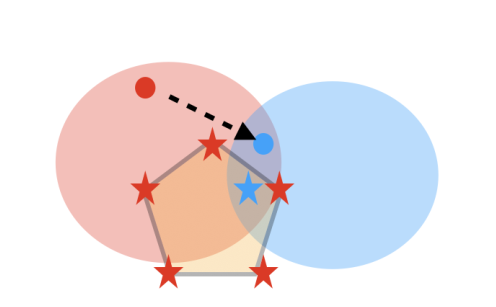
- 红色/蓝色分别代表在training/testing环境下好的策略
- 仅仅学习一个策略,可能导致繁华效果较差(红点或蓝点)
- 学习一个策略凸集,被anchor point约束(⭐顶点)
Problem Setting(Online Adaptation)
在$\mathcal M$上训练,在$\overline{\mathcal M}$上泛化,两个环境状态-动作空间相同,但是状态转换和奖励函数不同,训练时不知道测试环境的metadata
k-shot adaptation setting
将test phase分成两个阶段
- 模型在新环境上微调
- 模型在新环境上交互
Learning Subspaces of Policies
Motivations
环境特征中包含冗余和相关的特征,这样可以舍弃一些特征作为动作选择的输入,传统的rl方法可能会过度依赖noise feature$\to$选择不同的feature subset都可以学到策略
不仅基于冗余环境学习最优策略$\pi_\theta$,也在此基础上学习次优策略$\pi_{\theta^*}$。两种策略之所以不同是因为选择了不同的feature subset。在真实环境上测试选择较好的策略
Subspace of Policy
$\Theta$代表参数集合,选择一个子集$\overline \Theta \subset \Theta$和基于特定参数集合的策略集合$\overline \Pi = \{ \pi_\theta| \theta\in \overline \Theta\}$,假定$\overline\Theta$是$\Theta$的一个多面体,定义N个anchor参数$\overline \theta _1,\overline \theta_2,\cdots,\overline \theta_N$,任何参数中的点可以表示为anchor参数的仿射组合
- N代表参数空间的自由度
- 任何在$\overline \Theta$中的策略都是锚节点的仿射组合,可以认为两个不同的策略share parameters,这样做的好处是可以经验服用
Learning Algorithm
Loss function over the parameter subspace记作
多边形,因此可以选择各个顶点代替期望
代表在每个顶点处随机采样
希望最大化这个loss
Subspace collapse
避免所有策略被映射到参数空间上的同一点(鼓励策略的多样性),定义clusterloss
定义总的loss,在奖励尽量大的情况下差异尽量大
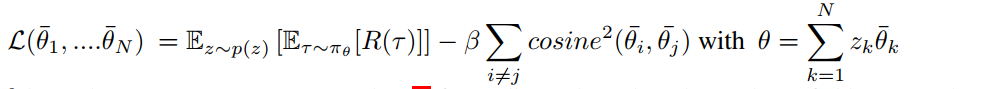
Line of Policies(LoP)
考虑两个策略的线性组合,给定锚点$\overline \theta_1,\overline \theta_2$,定义它们的线性组合为
z随机采样自$[0,1]$,这样损失函数为
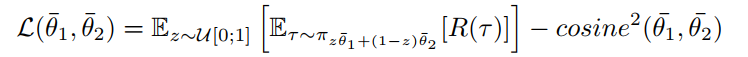
本质上还是鼓励策略的多样性
算法(两个策略)

$\overline\theta_1,\overline \theta_2$对应test environment上的两个策略网络
- 选择n个策略加权组合$(z_i,1-z_i)$
- 计算每个策略加权$\theta_{z_i} = z_i \overline \theta_1+(1-z_i)\overline \theta_2$
- 基于策略收集若干轨迹,更新策略(policy loss和策略差异)
- 更新critic(TD loss)
实验
在一个环境上训练在50个环境上泛化,在简单的控制任务上选择不同的物理参数作为环境的泛化
baseline
- 在训练环境上训练单个策略,在测试环境上评估(Single)
- 在训练环境上训练多个策略,根据DIAYN和task reward设置策略参数(DIAYN+r)
PPO-LoP
PPO为了减少分布偏移的影响,基于旧策略$\pi_{old}$生成的数据集评估新策略$\pi_\theta$上的性能
目标是
同时约束新旧策略差异
将其引入最大化目标中
实际应用中有两种策略
- 根据两次策略不同更新$\beta$,差异不大增大$\beta$,否则减少$\beta$
- 做截断,对于importance系数差异过大的部分舍去