duality explain
Convex Optimization(Duality from different perspectives)
回顾——对偶问题
原问题具有最优解$p^*$
Lagrange Function定义为
Dual Function定义为
Dual Problem定义为
定义的域是$\R^{m+p}$,它的解记作$d^*$
对偶问题具有两个重要结论
- 对偶问题是凸优化问题
- \leq p^p^*$
=p^=p^=p^=p^=p^=p^$满足的条件(对偶间隙$d^-p^*=0$)
定义——相对内部
原始优化问题域D的相对内部定义为
对于$\R^3$中的一个二维圆,显然每个点都是它的边界,但是除了圆的边缘,其它点都是相对内部
Slater条件(充分条件)
凸问题**,并且等式约束是仿射
满足如下条件时,对偶间隙为0
=d^=d^=d^=d^=d^=d^=d^=d^=d^=d^=d^$(严格满足不等式)
Weaker Slater Condition,若不等式约束也是仿射约束
= d^= d^= d^^*$
仿射约束在空间构成多面体,一定存在相对内点
$cx+d\leq 0$表示一个半空间,$cx+d<0$表示除了超平面以外的半空间,考虑D的相对内部,实际上
$relint D$实际上是$relint f_0 = relint\{dom f_0 \}$
- $f_0$定义在全空间上,则一定能满足Slater条件(多面体内部和超平面相交)
- $dom f_0$并非定义在全空间
因为假定可行解存在,一定能找到可行域D上的相对内点,和多面体内部相交
推论:线性规划(目标函数也是仿射)存在可行解,则对偶间隙为0
二次规划问题
一旦存在可行解,则对偶间隙为0,它的对偶问题是
是无约束二次规划
的解相同
QCQP,目标函数二次矩阵是正定的
Lagrange函数和对偶函数是
$\lambda_i \geq 0$时,$L(x,\lambda)$是x的凸函数
$\lambda \geq 0$时,$g(\lambda)$是凹函数
验证Slater条件,如果$\exists x\in D=\R^n$,满足
= d^ d^*$
若$ q_i = r_i=0$,则不存在x满足$x^T P_i x<0$,此时可行解只有$x= 0$,最优值为0,对偶问题最优值也是0(不满足Slater条件但是对偶间隙为0)
对偶间隙为0的解释
几何解释
仅包含不等式约束的优化
定义
最优值定义为
对偶函数定义为
$g(\lambda)$首先是$\lambda$的函数,对域中所有点$(u,t)$取$\lambda u + t$最小值
几何解释:现在二维区域上绘制出集合G,$p^*$即为落在u轴负半轴中t的最小值
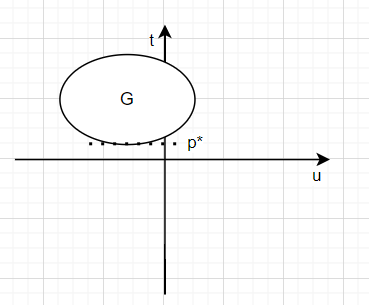
现在讨论对于某个$\lambda \geq 0,g(\lambda)$的几何含义,显然
代表一条直线,斜率是$-\lambda$,它在t轴上的截距为c,$g(\lambda)$对应的直线满足两个条件
- 与G至少有一个交点
- 在t轴上的截距尽量小
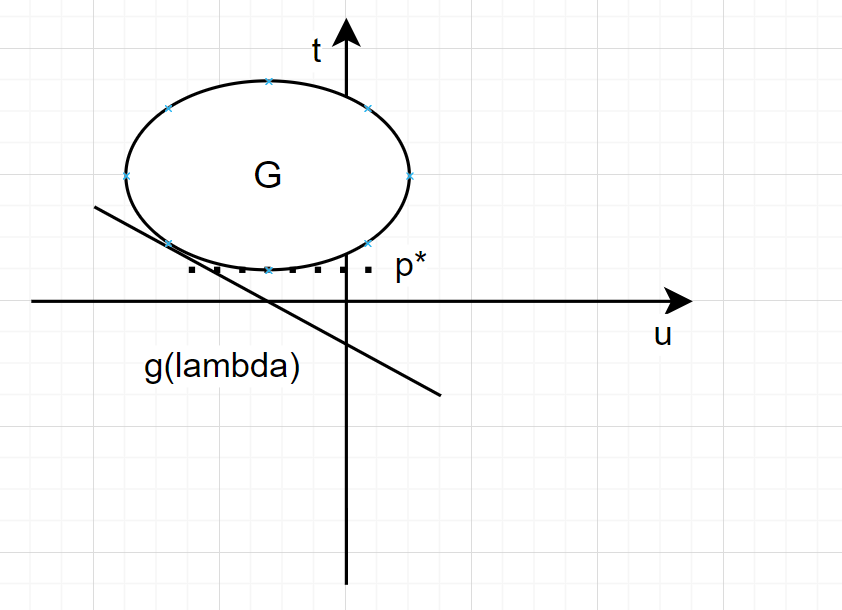
对偶问题的目标是
- 直线斜率为负
- 不断平移直线,使得截距逐渐提升(对于同一个$\lambda$,应该获得最小截距)
这种情况下可以看出来弱对偶一定成立
鞍点Saddle Point
对于原始问题的拉格朗日函数$L(x,\lambda)$,这个函数的鞍点定义为
,\lambda^mbda^*)$同时满足左右两侧
显然右侧对应$d^*$
考虑左侧,对应的
如果对于$x\in D,\forall i,f_i(x)<0$,则显然
如果$\exists i,f_i(x)>0$,则
考虑$\inf$,显然等价为
因此
如果能找到一个点同时满足左右两侧,则一定可以保证对偶间距为0
一般的函数$f(w,z),w\in S_w,z\in S_z$,一定有
何时等式成立并且对应的w,z相等?
称为函数的鞍点,显然鞍点等价的定义是
对偶问题中引入鞍点,拉格朗日函数
对$\lambda$求极大
否则$\sup_{\lambda\geq }L(x,\lambda)$为$\infty$
因此
对偶间距为0意味着
,\lambda^,\lambda^lambda^*)$同时满足左右两侧
鞍点定理
,\lambda^bda^*)$为$L(x,\lambda)$的鞍点,等价于
- 强对偶存在
- ,\lambda^bda^*)$为原始优化问题和对偶问题最优解
$\Rightarrow$显然(鞍点定义,强对偶存在),并且
进一步写成
因此$\lambda^*$为对偶问题最优解
,\lambda^,\lambda^,\lambda^,\lambda^bda^*)$
$\Leftarrow $,最优解一定是可行解,因此有
对偶间隙为0意味着
最后一步源自$f_i(x)\leq 0,\lambda_i \geq 0$,所有的不等式都是等式,因此有
上述第一个等式等价为
考虑如下定义
同时,根据(39)第二个等式可知
因此得到
,\lambda^,\lambda^*)$是对偶问题的解)
这实际上是鞍点的第二个定义
多目标优化
可以通过非负加权$\lambda_i$得到一组帕累托最优解
这是对应的单目标优化问题的拉格朗日函数$L(x,\lambda)$,给定$\lambda$,极小化
求出的极小值是$\lambda$函数$g(\lambda)$,在$\lambda\geq 0$上对g求极大,得到
带入$\hat \lambda$到$L(x,\lambda)$,并求解
得到的$\hat{\hat x}$实际上是$\hat\lambda $对应的帕累托最优面上的一组解,如果对偶间隙为0,则多目标优化在$\hat \lambda$下的最优解和$g(\lambda)$等价
经济学解释
产品产量x,$-f_0(x)$代表产品利润,目标
约束$f_i(x)\leq 0$表明生产x件产品第i类原材料不超过给定值
原材料可以交易,价格为$\lambda_i\geq 0$,剩余原材料卖出的利润是
这样目标是
$f_i(x)\geq 0$意味着要从市场买入原材料,这样
意味着自由市场一定比商品不能自由交换的社会更有效率(弱对偶)
现在讨论强对偶的条件,假设
*影子价格*影子价格*影子价格*影子价格*影子价格*影子价格影子价格格**
- )<0$,此时$\lambda_i^\lambda_i^*= 0$
- >0$,则$f_i(x^0$,则$f_i(x^*) = 0$