KKTcondition | Hexo

Convex Optimization(Duality IV—论对偶间距为0的若干推论，KKT条件)

互补松弛条件(对于一般优化问题，对偶间隙为0)

考虑一般优化问题(不一定凸)

$$\min f_0(x)\\ s.t \ f_i(x)\leq 0,i =1,2,\cdots,m\\ h_i(x)=0,i=1,2,\cdots,p$$

对偶函数

$$g(\lambda,v) = \inf_x \{f_0(x)+\sum_i \lambda_i f_i(x)+\sum_i v_i h_i(x) \}$$

对偶问题

$$\max g(\lambda,v)\\ \lambda \geq 0$$

做出两个假设

1. 对偶间隙为0
2. 假设所有函数可微

假设对偶问题和原问题最优解为

$$x^*,\lambda^*,v^*$$

必然是可行解，满足

$$f_i(x^*)\leq 0\\ h_i(x^*) =0\\ \lambda^*\geq 0$$

对偶间隙为0意味着

$$f_0(x^*) = g(\lambda^*,v^*) =\inf_x \{f_0(x)+\sum_i \lambda_i^* f_i(x)+\sum_i v_i^* h_i(x) \}$$

$\inf$满足

$$g(\lambda^*,v^*) \leq f_0(x^*) +\sum_i \lambda _i^* f_i(x^*)+\sum_i v_i^* h_i(x^*)\leq f_0(x^*)$$

对偶间距为00**的前提下，上述不等式全部是等式，即

1. ,\lambda^,v^) = g(\lambda^,v^^*)$
2. ,\lambda^,v^) = f_0(x^x^*)$

等式（2）表明对于不等式约束，必然有

$$\lambda_i^* f_i(x^*) = 0\to \lambda_i^* = 0 \or f_i(x^*) =0(\lambda_i^* =0)$$

互补松弛条件（Complementary Slackness）s）**

同时，等式（1）表明

$$x^* ={\arg\min}_x L(x,\lambda^*,v^*)$$

定义在全空间上的函数！*,$x^*,$x^$x^*$是L在全空间上的全局最优

根据可微条件，有

$$\frac{\partial L(x,\lambda^*,v^*)}{\partial x} =0$$

拆开看梯度

$$\nabla f_0(x^*) +\sum_{i=1}^m \lambda_i^* \nabla f_i(x^*) +\sum_{i=1}^p v_i^* \nabla h_i(x^*) = 0$$

这被称为stationary。对于得到的等式和不等式分成四类

原问题可行性

$$f_i(x^*)\leq 0\\ h_i(x^*) = 0$$

对偶问题的可行性

$$\lambda_i^* \geq 0$$

互补松弛条件(对偶间隙为0)

$$\lambda_i>0\to f_i(x^*) = 0$$

稳定性(函数可微)

$$\nabla f_0(x^*) +\sum_{i=1}^m \lambda_i^* \nabla f_i(x^*) +\sum_{i=1}^p v_i^* \nabla h_i(x^*) = 0$$

它们的关系是

graph LR
A[原问题可行性]
B[对偶问题可行性]
C[互补松弛条件]
D[稳定性]
A--对偶间距为0-->C
B--对偶间距为0-->C
C--可微-->D

这些条件被称为KKT条件

问题：KKT条件何时是充要条件？

定理：原问题满足三个条件，KKT条件是充要条件

1. 凸问题
2. 函数可微
3. 对偶间隙为0

下面证明充分性

,\lambda^,v^)$满足KKT条件$\Rightarrow,(x^,\lambda^,v^)$为对偶问题和原问题最优解

实际上只要证明

$$g(\lambda^*,v^*)= f_0(x^*)$$

（这是因为根据minmax定理，必然有$g(\lambda,v)\leq f_0(x)$），能取到等号已经是极限

可行性条件可以得到

$$L(x,\lambda^*,v^*) = f_0(x)+\sum_i \lambda_i^* f_i(x) +\sum_i v_i h_i(x)$$

,v^,v^,v^,v^,v^,v^,v^,v^,v^,v^^*)$关于x凸

凸函数一阶偏导0为全局最优

因此

$$L(x,\lambda^*,v^*) \geq L(x^*,\lambda^*,v^*)$$

考虑$g(\lambda,v)$，显然

$$\begin{aligned} g(\lambda^*,v^*)& =\inf_x L(x,\lambda^*,v^*)\\ &=L(x^*,\lambda^*,v^*)(上述证明说明x^*是L的全局最优)\\ &=f_0(x^*) +\sum_{i=1}^m \lambda^*_i f_i(x^*)+\sum_{i=1}^p v_i^* h_i(x) \end{aligned}$$

互补松弛条件，得到

$$\sum_{i=1}^m \lambda_i^* f_i(x^*) = 0$$

因此

$$g(\lambda^* ,v^*) = f_i(x^*)$$

得证

求解凸优化等价于求解KKT条件

优化问题之间的关系用一下表示

$$A=可微优化问题\\ B=凸并且可微优化问题,B\subseteq A\\ C=满足p^* =d^*的可微优化问题,C\subseteq A\\ C\bigcap B的问题KKT是充要条件$$

例子

半正定二次规划

$$\min \frac{1}{2}x^T P x+q^T x + r\\ s.t\quad Ax = b$$

写出KKT条件

$$Ax^* = b(primal)\\ \frac{\partial L}{\partial x^*} = P x^* +q + A{v^*}^T =0$$

两个线性方程，写成

$$\begin{pmatrix} P & A^T \\ A & 0 \end{pmatrix} \begin{pmatrix} x\\ v^* \end{pmatrix} = \begin{pmatrix} -q\\ b \end{pmatrix}$$

等价于求解线性方程组

约束改成 $Ax\geq b$，则会导致互补松弛条件极难求解

Water filling问题

变量是x，$\alpha$是参数，满足$\alpha_i> 0$

$$\min - \sum_{i=1}^n \log (\alpha_i+x_i)\\ s.t\ x\geq 0,1^T x = 1$$

KKT条件(primal)

$$x^* \geq 0\\ 1^Tx^* =1$$

对偶变量$\lambda^*$约束

$$\lambda^* \geq 0$$

互补松弛

$$\lambda^*_i x_i^* =0$$

微分条件，拉格朗日函数

$$L(x,\lambda^*,v^*) = -\sum_{i=1}^n \log (\alpha_i+x_i)-\lambda^*{x^*}^T +v^* (1^T x-1)$$

\in\R^n,v^\in\R^n,v^*\in \R$

求微分

$$\frac{\partial L}{\partial x_i} =- \frac{1}{\alpha_i + x_i}-\lambda^*_i+ v^*=0\\\ v^* =\lambda_i^*+\frac{1}{\alpha_i+x_i^*}$$

微分条件等价为

$$v^*(\alpha_i+x_i^*) =\lambda_i^*(\alpha_i+x_i^*)+1\Leftrightarrow\\ v^*(\alpha_i+x_i^*) = \lambda_i^* \alpha_i+1(\lambda_i^*x_i^*=0)\Leftrightarrow\\ \lambda_i^* =\frac{v^*(\alpha_i+x_i^*)-1 }{\alpha_i}\\ x_i^*=\frac{\lambda_i^* \alpha_i +1 -\alpha_i v^*}{\alpha_i}$$

$\lambda_i^*\geq 0$等价为

$$v^*(\alpha_i+x_i^*)-1\geq 0\to v^*\geq \frac{1}{\alpha_i +x_i^*}$$

\geq \frac{1}{\alpha_i}$，可以推导出$\lambda_i^ > 0$，则可知$x_i^i^* = 0$

< \frac{1}{\alpha_i}$，则可知$x_i^>0$，$x_i^ = \frac{1}{v^}-\alpha_i$（这是因为$x_i^>0$，必然有$\lambda_i^=0$）

1. \geq \frac{1}{\alpha_i}\to x_i^i^*=0$
2. <\frac{1}{\alpha_i}\to x_i^ =\frac{1}{v^^*}-\alpha_i$

算法（灌水算法）

绘制$\alpha_i - i$图像

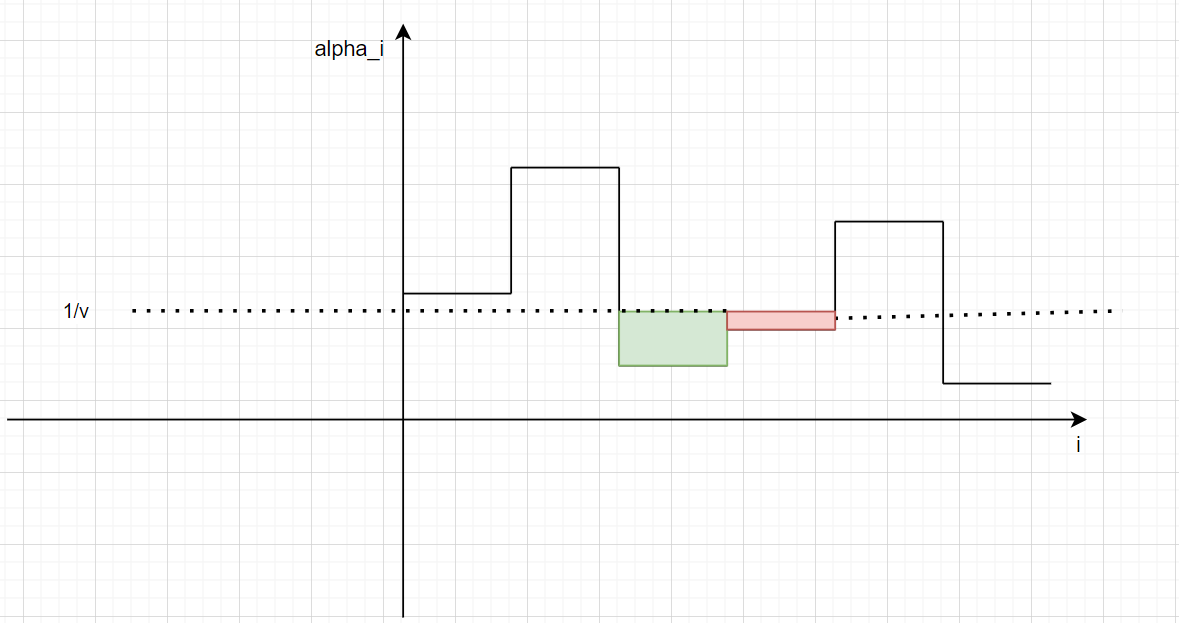
}$，在$\frac{1}{v^}$，在$\frac{1}{v^，在$\frac{1}{v^*}$以下的区域，$x_i$取值为图上着色正方形

什么时候得到最优解？

提升$\frac{1}{v^*}$(提升水面高度)，使得水面以下区域高度和之和为1(primal条件)

KKT条件和一阶最优性条件

对可微凸优化

$$\min f_0(x)\\ s.t \quad x\geq 0$$

最优性条件等价于

$$x\geq 0\\ \nabla f_0(x)\geq 0\\ x_i \nabla f_0(x)_i =0(Complementary)$$

x和$\nabla f_0(x)$互补

KKT条件

$$x^*\geq 0\\ \lambda^*\geq 0\\ \lambda_i^* x_i^* = 0\\ \nabla f_0(x^*) -\lambda^* = 0$$

$\lambda$和$x$互补，替换$\lambda^*$

$$\nabla f_0(x^*)x_i^* =0\\ \nabla f_0(x^*)\geq 0$$

凸问题等价形式

原问题有两种形式A,B，它们的对偶问题不一定相同

$$\min f_0(Ax+b)$$

$f_0$是凸函数

对偶问题是

$$L(x) = f_0(Ax+b)\\ g(\lambda,v) = \inf_x f_0(Ax+b)\\ \max g(\lambda,v) =\inf_x f_0(Ax+b)$$

=d^=d^*$(原问题和对偶问题完全相同)

现在考虑原问题的等价问题

$$\min f_0(y)\\ y=Ax+b$$

_1,d^_1,d^_1,d^_1,d^*_1$，写出对偶问题

$$L(y,x,v) = f_0(y) + v^T ( Ax+b-y) = f_0(y)- v^T y +v^T Ax+v^Tb \\ g(v) =\inf_{x,y} L(y,\lambda,v) \\ \inf_y (f_0(y)-v^Ty) =-\sup_y (v^T y -f_0(y)) =-f^*(v)(函数共轭)\\ \inf_x -v^T Ax-v^T b =-\infty(v^T A\neq 0),-v^T b(v^T A=0)$$

注意函数L(y,x,v)中y和x解耦，不存在约束，因此可以分别求极小

得到

$$g(v) =\left\{ \begin{aligned} & -f^*(v)-v^Tb ,v^TA =0\\ & -\infty,v^T A\neq 0 \end{aligned} \right.$$

对偶问题是

$$\max v^T b - f_0^*(v)\\ s.t\quad v^T A =0$$

对偶问题1和原始对偶问题有很大的不同

范数

$$\min \parallel Ax-v\parallel$$

等价问题

$$\min \parallel y\parallel\\ s.t\quad y = Ax -b$$

对偶函数

$$L(x,y,v) =\parallel y \parallel -v^T y +v^TAx -v^Tb\\ (引用上面讨论的结论) g(v) =\inf_{x,y}L(x,y,v) =\left\{ \begin{aligned} &-v^T b+\parallel v\parallel_*\\ &-\infty \end{aligned} \right.$$

因此对偶问题是

$$\max -v^T b -\parallel v\parallel_*\\ s.t\quad v^T A=0$$

值值和下列问题等价

$$\max\ v^T b-\parallel v\parallel_*\\ s.t\quad v^T A =0$$

可以理解为用w代替-v，得到

$$\max w ^T b -\parallel v\parallel_*\\ s.t\quad w^T A=0$$

因此这两个问题的值相同

对原问题还有一种变换

$$\min \frac{1}{2}\parallel y \parallel^2\\ s.t\quad Ax -b = y$$

解解*是等价的，这两个问题等价本质上来自于范数的非负性，因此约束目标实际上是等价的

$$\min \parallel y \parallel\Leftrightarrow\min \parallel y \parallel^2$$

它的对偶问题写成

$$L(x,y,v) =\frac{1}{2}\parallel y \parallel^2 +v^T (Ax - b -y)\\ g(v) =\inf_{x,y} L(x,y,v) =\left\{ \begin{aligned} & -v^T b-\frac{1}{2}\parallel v\parallel_*^2,v^T A =0\\ &-\infty ,v^TA \neq 0 \end{aligned} \right.$$

对偶问题是

$$\max -v^T b -\frac{1}{2}\parallel v\parallel_*^2\\ s.t\quad v^T A=0$$

约束目标不同

带框约束的线性规划问题

约束是高维空间的立方体

$$\min c^T x\\ s.t\quad Ax=b\\ l\leq x\leq u$$ $$\begin{aligned} L(x,\lambda_1,\lambda_2,v) &=c^T x +v^T(Ax - b)+\lambda_1^T (l-x)+\lambda_2^T (x-u)\\ &= (c^T +v^T A-\lambda^T_1+\lambda_2^T) x-v^T b +\lambda_1^T l-\lambda_2^T u \end{aligned}$$

对偶问题

$$\max -b^T v+\lambda_1^T l-\lambda_2^T u\\ s.t\quad A^T v+c^T -\lambda_1^T+\lambda_2^T =0,\lambda_1\geq 0,\lambda_2\geq 0$$

仍然是线性规划，对原问题做等价变换(将目标函数和框约束写成一个形式)

$$\min f_0(x)\\ s.t\quad Ax = b\\ f_0(x) =\left\{ \begin{aligned} &c^T x,l\leq x\leq u\\ &\infty ,else \end{aligned} \right.$$

这个问题对偶问题

$$L(x,v) =f_0(x)+v^T (Ax -b)\\ g(v) =\inf_x f_0(x)+v^T (Ax - b) = \inf_{x\in [l,u]} c^T x+v^T(Ax - b)$$

最终还是一个框约束的线性规划

$$g(v) =\inf_{x\in [l,u]} (A^Tv +c)^T x-v^T b$$

不包含等式约束让问题变得简单，观察

$$A^T v+c$$

这是一个n维向量，记作$(w_1,w_2,\cdots,w_n)$，显然，如果

1. $w_i\geq 0\to x_i = u$
2. $w_i<0\to x_i = l$

解记作

$$g(v) = -v^T v +l^T (A^T v +c)^+-u^T (A^T v+c)^-$$