Convex Optimization Convex Problems
Convex Optimization——Convex Problems
定义-优化问题
优化问题
优化问题的域
$dom f_0\bigcap dom f_i \bigcap dom h_i$
可行解feasible set
域中满足约束的点集$x_f$
最优值optimal value
$x_f=\phi\to p^*=\infty$
最优解(集)optimal set/point
$\epsilon$次优解集
并非要求目标函数最小(Satisificing solutions)
- 满足约束
- 目标函数取值与最优值距离不太远
局部最优解
$x$是局部最优解,则存在一个子集使得局部最优
找到一个球和可行解集的交集,满足在这个交集中最优
活动约束
若$ x\in x_f,f_i(x)=0$,则称$f_i(x)\leq 0$为活动约束
可行解在约束上取=
如果不存在$x\in x_f$,使得$f_i(x)=0$,则称$f_i(x)\leq 0$为non-active
能否将$\leq $改成$<0$
对于non-active约束是$\leq $和<是等价的,实际中可以将$<$变成$\leq$
原始约束$f_i(x)< 0$,修改成约束和域的交集
- $f_i(x)\leq 0$
- $-|\log {-f_i(x)}|\leq 0$
可行性优化问题
只需要找到可行解
广义上
- 目标函数是凸函数
- 约束在凸集上
优化问题的等价问题
盒子约束
约束写成
问题的缩放和变换
对原始约束问题做缩放
另一种等价形式,定义如下函数
- $\psi_0(\R\to \R)$单调递减
- $\psi_i,i=1,2,\cdots,m:\R\to \R$,满足$\psi_i(u)\leq 0\Leftrightarrow u\leq 0 $
- $\phi_i,i=1,2,\cdots,p,\R\to \R$,满足$\phi_i(u)=0\Leftrightarrow u = 0$
写出等价形式
消除等式约束$h_i(x)=0$
对于满足等式约束的情况,一定有
使得
$h_i(x) = 0$实际上构成一组方程组,那么满足这个方程组的解(假设x为n维向量,有p个约束),则它的解空间一定是n-p维的$\to$等式约束转化为某种升维映射
例子,对于$x\in \R^3$上的约束
写成$\R\to \R^3$的映射$\phi$,满足
有两条结论
- \phi(z) = x$
- $\forall z\in \R,x=\phi(z)$满足等式约束
进一步去掉这个约束
消除线性等式约束
Ax=b无解,无意义
$x= A^{-1}b$,解空间上只有一个点
一般情况,求出$Ax =b$化0空间上的所有向量,假设有m个$z_1,z_2,\cdots,z_m\in \R^n$,满足$Az_i=0$,此时构造$\mu \in \R^m$,并且$Ax =b$有一组特解$x_0$,解写成
定义-凸优化问题
- 目标函数是凸函数
- 不等式约束的左边是凸函数$\to 0-sublevel$ set是凸集
- 等式约束是仿射函数$a_i^T x=b_i$,仿射集合构成凸集
基于仿射约束对问题降维
一组线性等式约束
等价于
因此写成
仿射不等式约束进行升维
假设$f_i(x)$也是仿射变换
松弛变量松弛变量松弛变量松弛变量**
为什么要假定$f_i(x)$也是仿射变换?如果非仿射变换能否引入松弛变量得到等价问题?
properity of convex problem
局部最优=全局最优
满足局部最优
假设x不是全局最优$\exists y\in x_f,s.t f_0(y)< f_0(x)$,则
构造z,满足
必然$z\in x_f(x_f是凸集)$,并且凸函数有
同时
z应该落在邻域内,但是$f_0(z)< f_0(x)$,矛盾
目标函数可微
可微函数满足一阶条件
在凸优化问题中,还应该约束
则
如果能找到$\nabla f_0(x^*)^T = 0$并且落在可行域内,则一定为最优解
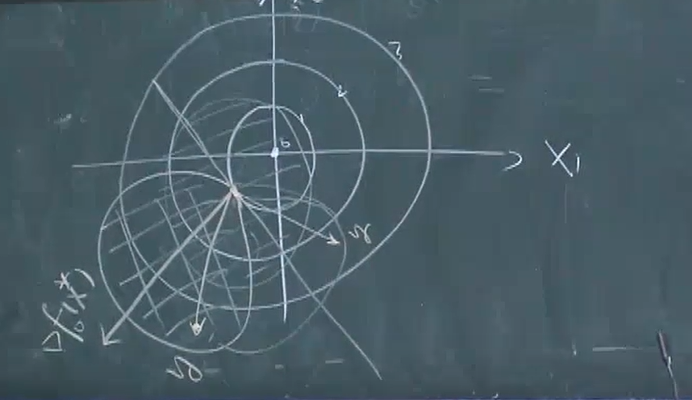
登高线登高线登高线*
$处取一个集合和这个等高线相交,并且集合C内任意一点x都有$f(x)\geq f(x^)=c$,则$\nabla f^T(x^)$必然在$x^$处和等高线相切,并且$\forall y\in C,\lang \nabla f(x^x^*),y-x\rang\geq $0
只包含等式约束的凸问题
根据最优条件,在最优点$x^*$上有
并且有$Ax^*=b$,则y写成
$\forall y\in \{y|Ay =b\}$都有(34),则(34)等价于
如果$rank(A)\leq n$,必然有
梯度方向和矩阵$\mathcal N(A)$空间正交
一个$\R^n$上的函数添加一个线性约束$Ax =b$,实际上相当于从某个维度对函数做了切分(可以考虑n=2在变量平面上画一条线的情况),此时最优解必然处在等高线和线性约束相切的位置
$f_0(x)=x_1^2 +x_2^2,x_1+x_2=1$,$\mathcal N(A)$空间满足
对于等高线
与$x_1+x_2=1$只有一个位置相交,满足
只有唯一解,等价于
等价于$c=\frac{1}{2}$,在$(1/2,1/2)$处梯度为$(1,1)$,必然与$\mathcal N(A)$正交
仅包含非负约束
一阶条件,$x^*$最优有
若$\nabla f^T(x^*)< 0$
梯度每个分量都小于0,则在$\geq 0$的半空间内必然可以让$\nabla f^T(x^*)y$取到无穷小,(44)必然不能被满足
因此必然有$\nabla f^T(x^*)\geq 0$
若$x=(x_1,x_2,\cdots,x_n)$且$f_0(x)$为线性函数,则$f_0(x)$可以写成
令$y=0$,有
)\geq 0,x^)\geq 0,x^ 0,x^*\geq 0$,则
因此必然有
得到,如果$x^*=(x_1,x_2,\cdots,x_n)$是最优解,则一定满足以下三个条件(实际上这是等价条件)
- $x\geq 0$
- $\nabla f_0(x)\geq 0$
- 如果$x_i\neq 0$,则$(\nabla f_0(x))_i$=0
互补条件,$x,\nabla f_0(x)$对应分量当且最多仅有一个非零元素(不可能出现$x_i\neq 0,\nabla f(x)_i\neq 0$)
几何上看这个结论
对于$\R^2$上的函数,如果约束在$\R_{++}^2$上求解最优化问题
最优点为$x_1=1,x_2=0$,最优值为1,在$(1,0)$处的梯度为
满足互补
典型的凸问题
凸问题的狭义定义
等式约束为仿射函数
线性规划
feasible set是凸的(多面体),Ax$\leq b$将全空间划分出一个子空间,不等式约束在子空间中切出一部分
对于目标函数也为仿射函数,最优解一定能在顶点取到
等价变换
S是松弛变量
等式约束全部为仿射,不等式约束要求在半空间,线性规划写成
分开X中正负元素,$X=X_+-X_{-},X_+\geq ,X_-\geq 0$
一定是等价问题
- 原问题中任意可行解可以在等价问题中找到对应可行解,并且目标函数值相同
- 等价问题中任意解可以在原问题中找到可行解使得函数值相同
食谱问题
人需要m种营养物质,每样物质不小于$b_1,b_2,\cdots,b_m$,第i种食物包含第j类营养物质的含量为$a_{ij},i=1,2,\cdots,n,j=1,2,\cdots,m$,价格为$c_1,c_2,\cdots,c_n$
线性分数规划
原问题的约束和线性规划相同,目标函数是线性分数函数
$f_0(x)$本身不是凸函数,例如
显然非凸
变成凸问题,写出等价线性规划,假设可行域不是空集,即
不是空集,写出它的等价形式
引入非负变量$z$,变成$\R^{n+1}$上的优化问题
证明优化问题的等价性
$,等价问题feasible set是$y_f^题feasible set是$y_f^*$,目的是说明
反之也需要成立
$\Rightarrow,\forall x\in x_f^*,y=\frac{x}{e^T x +f},z=\frac{1}{e^T x+f}$
先证明$(y,z)\in y_f^*$
同时
得证
假设$z\geq 0$假设$z\geq 0$\geq 0$**,定义
x是原问题的可行解,且函数值相同
考虑$z=0$的情况,若$(y,0)$是等价问题的可行解,假设$x_0\in x_f^*$是原问题的一个可行解,尝试证明
是原问题的一个可行解,因为$z=0$是等价问题的可行解,因此有
考虑$x= x_0+ty$
计算
希望找到t,使得
令$t\to \infty$即可
证明极限等价于证明了存在性么?
二次规划
最优解可能在集合内部(二次函数最小值在多面体内取到)
二次约束二次规划(QCQB)
约束也是二次规划
带噪声的测量系统
x是测量值,带有噪声e,求解的物理量y和x之间的关系满足
目标写成
最优解为
关于x的先验知识
x稀疏
0-范数不是凸函数,改写成1范数 $L_1$ regularized
消除绝对值,切分
原始损失函数改写成
变成$\R^{2n}$上的凸优化问题,转化为光滑的问题
变成
Ridge regression(x中元素类似)
减少数据的方差,二次项系数为
一定是正定的$\lambda_2\geq 0$
它的等价形式为
有如下结论
$\forall \lambda_2\geq 0,\exists \theta \geq 0,s.t x\in \R^n$同时满足原问题和对偶问题的最优解
直观上理解这个问题,对于原问题
假设$x= \hat x$使得原问题取得最优解,则令
验证$x = \hat x$同时满足对偶问题的最优解,假设对偶问题存在更优解$\hat x^\prime$,使得在满足
的前提下,满足
此时将得到
$x^\prime$是原问题的最优解,矛盾。Q.E.D
变成QCQP问题
投资组合问题
总的资金数量B,有n种投资方案,分别投资$x_1,x_2,\cdots,x_n$,一定时间后获得回报为$p_1x_1,p_2x_2,\cdots,p_nx_n$
显然问题不等式取=得到等价问题
这个模型过于简化,$p_i$往往未知,一个可靠的投资需要满足
- 收益高$p_i$较高
- 风险低$p_i$方差较低
假设$\overline p$是p的期望组成的向量,$\sum$为协方差矩阵,假设是一个对角矩阵$diag(a_1,a_2,\cdots,a_n)$,新的投资组合模型为在奖励最大的情况下极小化风险(奖励满足某个下界)
这里引入$r_\min$用于最大化奖励,和$l_1$正则化技巧类似
半正定规划
约束是仿射变换(矩阵上的线性规划)
对角矩阵$C,X$,对角矩阵对角元素组成向量$diag(\cdot)$
另一种形式,对向量的优化(基于半正定矩阵的分解)
不等式约束中的$\leq$表示的是$x_1A_1+\cdots+x_nA_n-B$是半负定矩阵,$x=(x_1,x_2,\cdots,x_n)$不等式约束表明的是矩阵线性组合
线性矩阵函数
考虑线性矩阵函数
定义矩阵谱范数$\parallel A(x)\parallel_2$为矩阵$A(x)$最大的奇异值(实际上是$A(x)^T A(x)$的特征值开根号),优化目标是
引理(奇异值不等式)
最大最大特征值,因此一定是半负定的,满足不等式$\parallel A(x)\parallel_2\leq \sqrt S$的不等式奇异值不超过$\sqrt S$(实际上意味着存在奇异值为$\sqrt S$的矩阵$A(x)$)
改写上述优化问题,写成
引入新变量S,考虑约束是否为凸,考虑$f(x) = A^T(x)A(x) -SI= (A_0 + x_1 A_1 +\cdots,x_n A_n)^T (A_0 +x_1 A_1+\cdots+x_n A_n)-SI$,证明它关于x,s联合凸
假设$(x,s_1),(y,s_2)$满足
显然$\theta s_i I -\theta s_i I$是负定矩阵,因此这种情况下还是负定的
令$\sqrt s=t$,写成(使得目标函数是线性函数)
写成$2q\times 2q$矩阵
两个约束等价,但是约束对$(x,t)$并不联合保凸,只对$(x,t^2)$联合凸
问题变成(优化变量为x,t,Y),下面的问题中等式约束是仿射的,不等式约束是凸的
多目标优化
考虑映射到向量空间的目标函数
希望同时极小化q个变量
多目标形式的投资组合
定义 Pareto optimal front
在某一个方向上增加,必然在某个方向上减少
Oracle Solution
,f_{02}^,f_{02}^,f_{02}^,\cdots,f_{0q}^*)$,实际上不一定能取到
等价的单目标优化问题
若$f_0(x)$在$\R^k$中为凸,$f_i(x)$为凸,$h_i(x)$为仿射,则可以求解下列问题求出pareto optimal front上点
实际上可以在$\R_+^q$上遍历所有点找到pareto optimal front上所有点
Ridge Regression
对应的多目标优化问题
$\lambda =0$相当于只有第一项优化,$\lambda =\infty$相当于只有第二项优化,Ridge Regression可以通过引入一个变量解决
对于$\forall \lambda$都可以找到对应的$\epsilon$,使得两个解相同
引子:拉格朗日乘子,当只需要优化$\parallel b-Ax\parallel_2$,即$\lambda =0$时,设置$\epsilon = \infty$即可
Quasi convex problem
- 不等式约束是凸函数
- 等式约束是仿射函数
- 目标函数是Quasi convex的